Wysokość graniastosłupa prawidłowego czworokątnego jest równa 16. Przekątna graniastosłupa

Wysokość graniastosłupa prawidłowego czworokątnego jest równa \(16\). Przekątna graniastosłupa jest nachylona do płaszczyzny jego podstawy pod kątem, którego cosinus jest równy \(\frac{3}{5}\). Oblicz pole powierzchni całkowitej tego graniastosłupa.

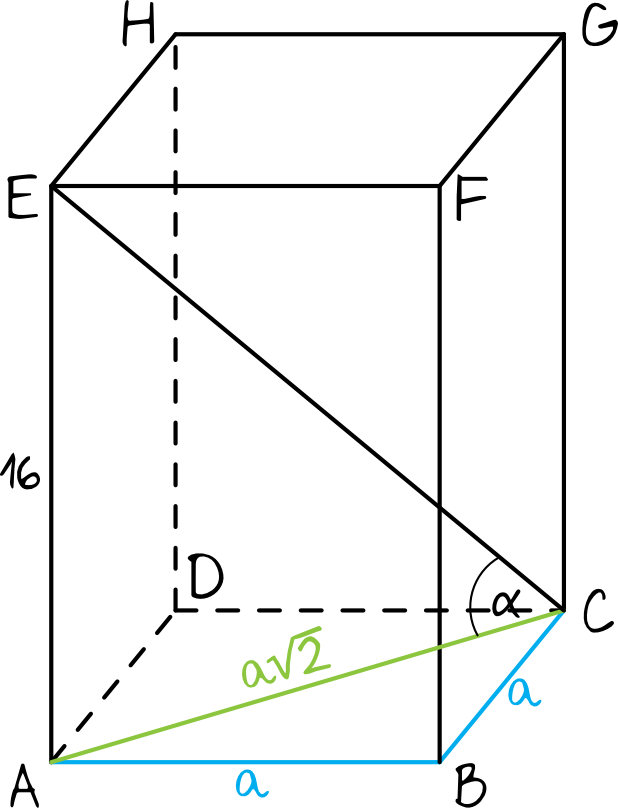
W zadaniu mowa o graniastosłupie prawidłowym czworokątnym, a to oznacza, że w podstawie znajduje się kwadrat. Jeśli więc bok kwadratu oznaczylibyśmy sobie jako \(a\), to przekątna \(|AC|=a\sqrt{2}\).

Kluczem do rozwiązania tego zadania będzie poznanie długości \(a\), bo wtedy obliczymy pole podstawy i pola ścian bocznych.

Spójrzmy na trójkąt \(ACE\). Znamy długość \(|AE|=16\). Wiemy też, że \(|AC|=a\sqrt{2}\). Gdyby więc udało nam się jeszcze ustalić długość odcinka \(|EC|\) to długość \(a\) obliczylibyśmy z Twierdzenia Pitagorasa.
Z pomocą przyjdzie nam informacja mówiąca o tym, że \(cosα=\frac{3}{5}\).
$$cosα=\frac{|AC|}{|EC|} \\
\frac{3}{5}=\frac{a\sqrt{2}}{|EC|} \quad\bigg/\cdot\|EC|\\
\frac{3}{5}|EC|=a\sqrt{2} \quad\bigg/\cdot\frac{5}{3} \\
|EC|=\frac{5\sqrt{2}a}{3}$$

$$a^2+b^2=c^2 \\
|AC|^2+|AE|^2=|EC|^2 \\
(a\sqrt{2})^2+16^2=\left(\frac{5\sqrt{2}a}{3}\right)^2 \\
2a^2+256=\frac{50a^2}{9} \cdot|\cdot9 \\
18a^2+2304=50a^2 \\
-32a^2+2304=0 \quad\bigg/:(-32) \\
a^2-72=0$$

Powstałe równanie możemy obliczyć metodą delty (pamiętaj, że w tym przypadku współczynnik \(b=0\)), ale wygodniej będzie zapisać to w ten sposób:
$$a^2-72=0 \\
a^2=72 \\
a=\sqrt{72} \quad\lor\quad a=-\sqrt{72}$$

Ujemne rozwiązanie oczywiście odrzucamy. To co jeszcze warto zrobić, to wyłączyć wspólny czynnik przed znak pierwiastka, tak więc:
$$a=\sqrt{72}=a=\sqrt{36\cdot2}=6\sqrt{2}$$

Znając długość \(a=6\sqrt{2}\) możemy już bez przeszkód obliczyć pole całkowite graniastosłupa.
$$P_{c}=2P_{p}+4P_{b} \\
P_{c}=2\cdot a^2+4\cdot a\cdot H \\
P_{c}=2\cdot(6\sqrt{2})^2+4\cdot6\sqrt{2}\cdot16 \\
P_{c}=2\cdot72+384\sqrt{2} \\
P_{c}=144+384\sqrt{2}$$

\(P_{c}=144+384\sqrt{2}\)