Aby móc rozwiązywać niektóre zadania z trygonometrii musimy umieć posługiwać się tablicami trygonometrycznymi z których będziemy odczytywać różne interesujące nas informacje. Tablice trygonometryczne znajdują się na końcu oficjalnych tablic matematycznych CKE, którymi posługujemy się na lekcjach matematyki oraz na maturze. Takie tablice znajdziesz tutaj:
Spójrzmy na konkretnych przykładach gdzie mogą przydać nam się tablice trygonometryczne:
Wiemy, że sinus kąta \(α\) wynosi \(\frac{3}{5}\), czyli \(0,6\). Musimy teraz skorzystać z tablic matematycznych i sprawdzić jakiemu kątowi odpowiada sinus o wartości zbliżonej do \(0,6\). Nas będzie interesował konkretnie ten fragment tablic:
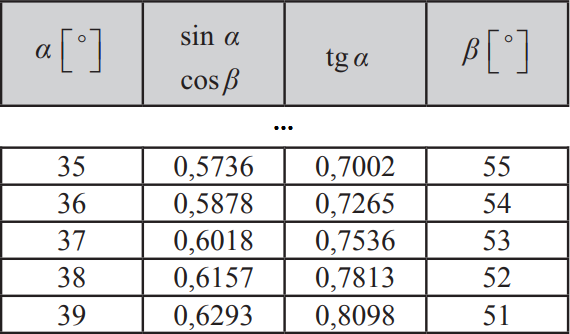
Szukamy odpowiedzi na pytanie dla jakiego kąta alfa sinus przyjmuje wartość równą \(0,6\). Jak widzimy – w tablicy nie znajdziemy idealnie wartości \(0,6\), a najbliżej tego jest wartość \(0,6018\). Z lewej strony odczytujemy, że sinus przyjmuje wartość \(0,6018\) dla kąta \(37°\), zatem możemy zapisać, że nasz kąt ma w przybliżeniu wartość \(α\approx37°\).
Ponownie musimy odnaleźć odpowiednią wartość w tabeli trygonometrycznej i tu także widzimy, że idealnej wartości \(0,6\) niestety nie znajdziemy:

Z powyższego fragmentu tablicy trygonometrycznej wynika, że najbliżej znajduje się wartość \(0,6018\) (czyli jest to dokładnie ta sama sytuacja co w pierwszym przykładzie). Z pozoru więc obydwa przykłady wydają się identyczne, jednak na tym podobieństwa się kończą, bo tym razem nie będzie to w przybliżeniu kąt \(37°\). W tablicach trygonometrycznych wartości kątowe cosinusów odczytujemy z prawej strony, z kolumny dla kątów beta. Mówi nam o tym nagłówek tabeli w którym pojawia się zapis \(cosβ\). To właśnie odczytywanie cosinusów sprawia najwięcej problemów, zwłaszcza kiedy sugerujemy się tym, że w treści zadania pojawia się kąt \(α\). Niezależnie od oznaczeń które pojawiają się w treści zadania my musimy odczytywać kąty zgodnie z nagłówkami tabeli, czyli dla sinusów i tangensów kąty alfa (lewa kolumna), a dla cosinusów kąty beta (prawa kolumna). To oznacza, że tym razem \(α\approx53°\).
Ponownie szukamy wartości \(0,6\), ale tym razem musimy spojrzeć na kolumnę tangensów:
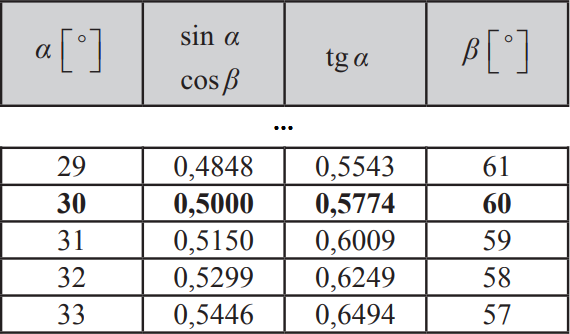
Przybliżenie jakie możemy znaleźć jest niemal idealne, bo pojawia nam się w tabeli wartość \(0,6009\). Spoglądamy na lewą kolumnę z wypisanymi kątami i widzimy, że tę wartość \(0,6009\) tangens osiąga dla kąta \(31°\), zatem możemy zapisać że \(α\approx31°\).
Korzystanie z tablic trygonometrycznych może się także odbywać w drugą stronę, czyli mając dany kąt możemy odczytać jaką wartość przyjmuje sinus, cosinus lub tangens.
Na początku możemy odczytać wartości sinusa oraz tangensa, bo wystarczy że w lewej kolumnie tabeli trygonometrycznej odnajdziemy wartość \(α=16°\).
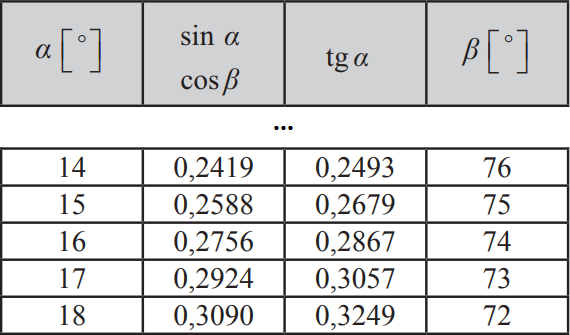
Z tabeli jasno wynika, że sinus dla kąta \(16°\) przyjmuje wartość \(0,2756\), natomiast dla tangensa przyjmuje wartość \(0,2867\), czyli matematycznie zapisując:
$$sin16°=0,2756 \\
tg16°=0,2867$$
Została nam jeszcze do określenia wartość cosinusa. Tym razem razem szukamy w prawej kolumnie wartości \(β=16°\), bo zgodnie z nagłówkami tabeli mamy zapisane w niej wartości cosinusa dla kątów beta.
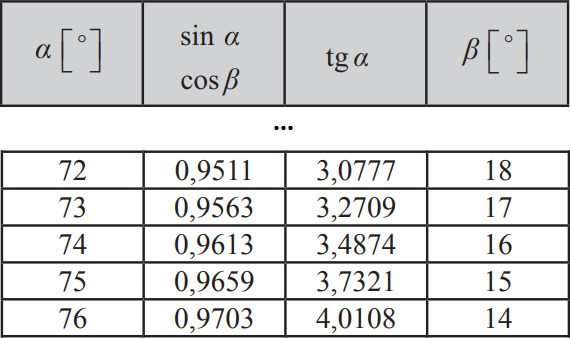
Zgodnie z tą tabelką możemy stwierdzić, że cosinus dla kąta \(16°\) przyjmuje wartość \(0,9613\), czyli:
$$cos16°=0,9613$$
Na matematyce (zwłaszcza na poziomie podstawowym) mimo wszystko najczęściej będziemy posługiwać się bardziej charakterystycznymi kątami, takimi jak \(30°, 45°, 60°\) lub \(90°\). Ich wartości znaleźć możemy nie tylko w tej klasycznej tabeli wartości trygonometrycznych, ale także w tak zwanej małej tabelce trygonometrycznej (także znajdziemy ją w tablicach matematycznych). To co jest ogromną przewagą małej tabelki to fakt, że zapisane są w niej dokładne (a nie przybliżone) wartości funkcji dla danych kątów. To właśnie dlatego znajdziemy tu zapisy liczb w postaci ułamków lub pierwiastków.
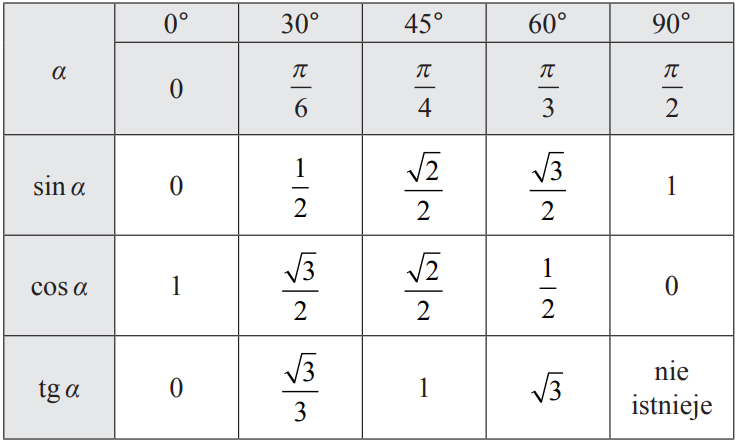
Umiejętność stosowania tej tabelki jest niezwykle istotna, bowiem dzięki temu że znajdują się w niej dokładne zapisy będziemy mogli w różnorodnych zadaniach skracać lub wymnażać poszczególne liczby.
Odczytywanie informacji z małej tabelki trygonometrycznej jest już niezwykle proste, tutaj nie ma żadnych haczyków, zatem możemy zapisać:
$$sin30°=\frac{1}{2} \\
cos30°=\frac{\sqrt{3}}{2} \\
tg30°=\frac{\sqrt{3}}{3}$$
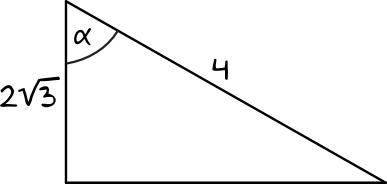
To zadanie jest klasycznym przykładem wykorzystania umiejętności zapisywania funkcji trygonometrycznych i odczytywania miar kątów z tablic.
Krok 1. Obliczenie wartości cosinusa.
Znamy długość boku leżącego przy kącie alfa oraz długość przeciwprostokątnej, czyli możemy bez przeszkód obliczyć wartość cosinusa.
$$cosα=\frac{2\sqrt{3}}{4}=\frac{\sqrt{3}}{2}$$
Krok 2. Odczytanie miary kąta z tablic trygonometrycznych.
Skorzystamy tutaj z małych tablic:

Okazuje się, że cosinus przyjmuje wartość \(\frac{\sqrt{3}}{2}\) dla kąta \(α=30°\) i to jest poszukiwana przez nas miara.
