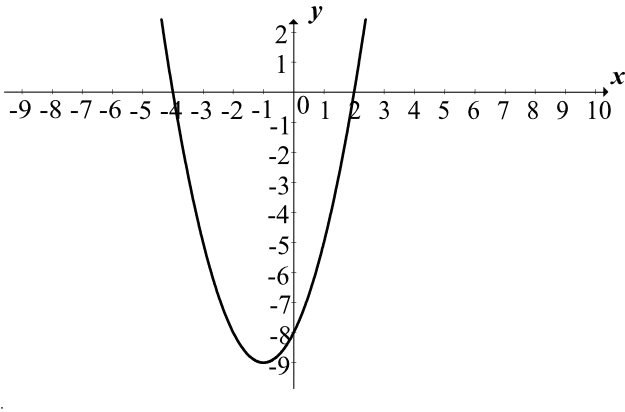Wskaż rysunek, na którym przedstawiony jest wykres funkcji kwadratowej, określonej wzorem \(f(x)=(x-2)(x+4)\).
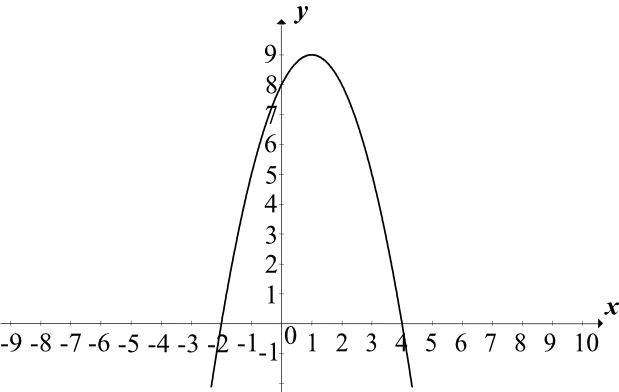
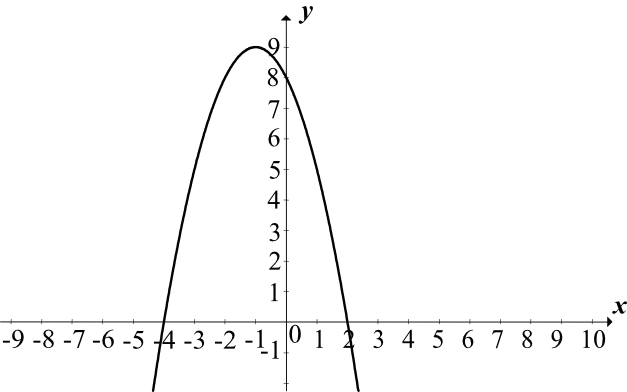
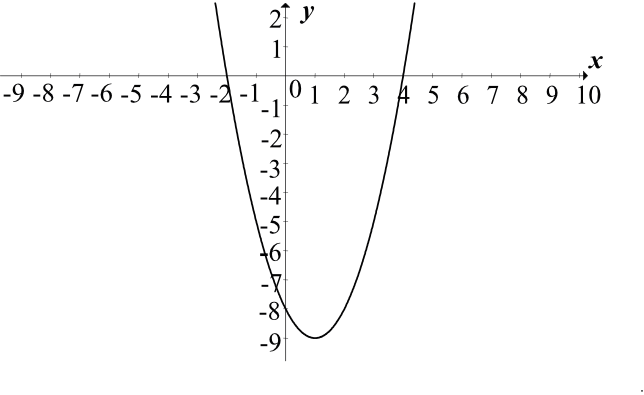
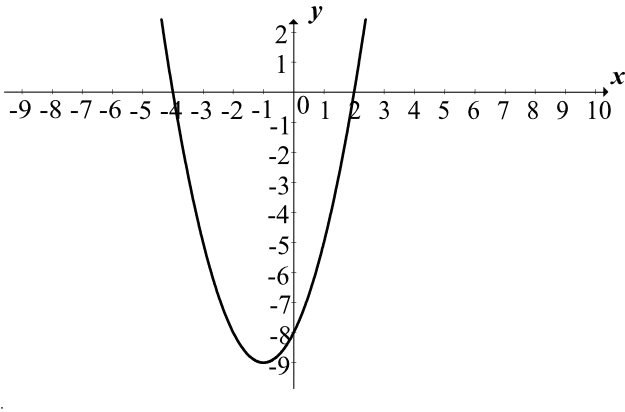
Rozwiązanie:
Krok 1. Wyznaczenie miejsc zerowych funkcji.
Mamy podaną funkcję w postaci iloczynowej, dzięki czemu w bardzo łatwy sposób możemy wyznaczyć jej miejsca zerowe.
$$(x-2)(x+4)=0 \\
x-2=0 \quad\lor\quad x+4=0 \\
x=2 \quad\lor\quad x=-4$$
Krok 2. Szkicowanie wykresu paraboli.
Nasza funkcja kwadratowa po wymnożeniu poszczególnych wyrazów będzie miała przy \(x^2\) współczynnik dodatni \(a=1\), więc ramiona paraboli będą skierowane ku górze.
To oznacza, żę szukamy funkcji, która ma miejsca zerowe \(x=2\) oraz \(x=-4\) i która ma ramiona skierowane do góry. Taka parabola znalazła się w czwartej odpowiedzi.
Odpowiedź: