Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy zwizualizować sobie jak ten czworokąt będzie wyglądać i gdzie będzie miał punkt przeciecia się przekątnych:
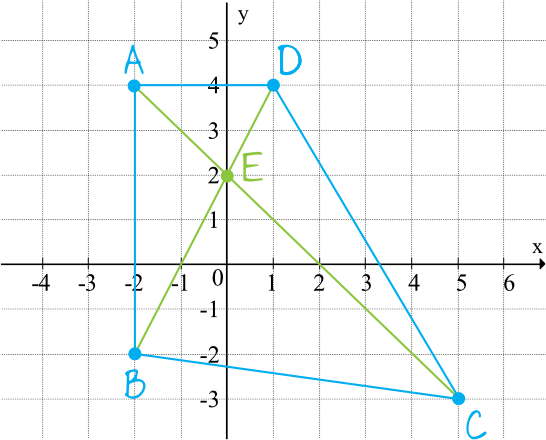
Z pomocą tego rysunku możemy określić plan postępowania: musimy wyznaczyć równania prostych \(AC\) oraz \(BD\), a następnie z równań tych prostych ułożyć układ równań, którego wynikiem będą współrzędne poszukiwanego punktu przecięcia.
Krok 2. Wyznaczenie równania prostej \(AC\).
Wyznaczmy równanie prostej \(AC\), czyli prostej przechodzącej przez punkty \(A\) oraz \(C\), czyli przez które tworzą jedną z przekątnych czworokąta. Możemy to zrobić za pomocą wzoru z tablic, czyli:
$$(y-y_{A})(x_{C}-x_{A})-(y_{C}-y_{A})(x-x_{A})=0$$
Do tego wzoru wystarczy tylko podstawić współrzędne punktów \(A\) oraz \(C\) i otrzymamy poszukiwany wzór. Istnieje też drugi sposób na wyznaczenie równania prostej, który jest nieco szybszy i właśnie z niego tutaj skorzystamy. Aby wyznaczyć prostą w postaci \(y=ax+b\) przechodzącą przez dwa punkty wystarczy stworzyć prosty układ równań, w którym podstawimy po kolei współrzędne obydwu punktów. I tak oto otrzymujemy:
$$\begin{cases}
4=-2a+b \\
-3=5a+b
\end{cases}$$
Odejmując to równanie stronami otrzymamy:
$$7=-7a \\
a=-1$$
Znając współczynnik \(a\) możemy teraz podstawić tę wartość do jednego z równań, wyznaczając tym samym współczynnik \(b\):
$$4=-2a+b \\
4=-2\cdot(-1)+b \\
4=2+b \\
b=2$$
To oznacza, że nasza prosta \(AC\) przyjmuje postać \(y=-1x+2\), czyli \(y=-x+2\).
Krok 3. Wyznaczenie równania prostej \(BD\).
Postępujemy analogicznie jak w przypadku prostej \(AC\), podstawiając tym razem współrzędne punktów \(B\) oraz \(D\):
$$\begin{cases}
-2=-2a+b \\
4=1a+b
\end{cases}$$
Odejmując to równanie stronami otrzymamy:
$$-6=-3a \\
a=2$$
Znając współczynnik \(a\) możemy teraz podstawić tę wartość do jednego z równań, wyznaczając tym samym współczynnik \(b\):
$$-2=-2a+b \\
-2=-2\cdot2+b \\
-2=-4+b \\
b=2$$
To oznacza, że nasza prosta \(BD\) przyjmuje postać \(y=2x+2\).
Krok 4. Wyznaczenie miejsca przecięcia się przekątnych.
Rozwiązaniem układu równań dwóch prostych są współrzędne punktu ich przecięcia (czyli dokładnie to czego szukamy). W związku z tym musimy stworzyć układ równań z dwóch równań prostych wyznaczonych przed chwilą i sprawdzić jakie współrzędne otrzymamy:
$$\begin{cases}
y=-x+2 \\
y=2x+2
\end{cases}$$
Korzystając z metody podstawiania otrzymamy:
$$-x+2=2x+2 \\
-3x=0 \\
x=0$$
Znając iksa możemy teraz obliczyć igreka, podstawiając \(x=0\) do jednego z równań:
$$y=-x+2 \\
y=-0+2 \\
y=2$$
To oznacza, że współrzędne punktu przecięcia się przekątnych są równe \((0;2)\).