Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Rozwiązywanie zadania rozpocznijmy od narysowania układu współrzędnych i zaznaczenia na nim danych z treści zadania:
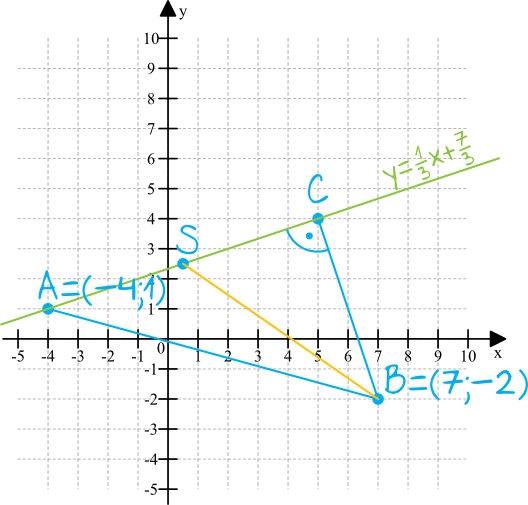
Krok 2. Wyznaczenie równania prostej \(BC\).
Z rysunku wynika, że prosta o równaniu \(y=\frac{1}{3}x+\frac{7}{3}\) przechodzi przez bok \(AC\). Widzimy też, że prosta \(BC\) jest prostopadła do tej prostej, a to pozwoli nam wyznaczyć współczynnik kierunkowy \(a\) prostej \(BC\). Dwie proste są względem siebie prostopadłe tylko wtedy, gdy iloczyn ich współczynników kierunkowych jest równy \(-1\). Skoro pierwsza prosta ma \(a=\frac{1}{3}\), to druga prosta będzie mieć \(a=-3\), bo \(\frac{1}{3}\cdot(-3)=-1\). To oznacza, że prosta \(BC\) wyraża się wzorem \(y=-3x+b\). Do poznania pełnego wzoru musimy jeszcze tylko wyznaczyć współczynnik \(b\) tej prostej.
Współczynnik \(b\) prostej \(BC\) wyznaczymy podstawiając do postaci \(y=-3x+b\) współrzędne jednego z punktów, który do tej prostej należy. Podstawiając zatem współrzędne punktu \(B=(7,-2)\) otrzymamy:
$$y=-3x+b \\
-2=-3\cdot7+b \\
-2=-21+b \\
b=19$$
To oznacza, że prosta \(BC\) wyraża się równaniem \(y=-3x+19\).
Krok 3. Wyznaczenie współrzędnych punktu \(C\).
Punkt \(C\) jest miejscem przecięcia się prostej \(AC\) oraz prostej \(BC\). Z geometrycznej interpretacji układu równań wiemy, że tworząc układ równań składający się z dwóch prostych otrzymamy miejsce ich przecięcia się. W związku z tym musimy rozwiązać następujący układ równań:
$$\begin{cases}
y=\frac{1}{3}x+\frac{7}{3} \\
y=-3x+19
\end{cases}$$
Ten układ równań najprościej będzie rozwiązać korzystając z metody podstawiania. Otrzymamy wtedy:
$$\frac{1}{3}x+\frac{7}{3}=-3x+19 \\
3\frac{1}{3}x=16\frac{2}{3} \\
\frac{10}{3}x=\frac{50}{3} \\
x=5$$
Znamy już wartość współrzędnej iksowej punktu \(C\), a współrzędną igrekową obliczymy podstawiając \(x=5\) do dowolnego z równań (np. drugiego), zatem:
$$y=-3x+19 \\
y=-3\cdot5+19 \\
y=-15+19 \\
y=4$$
To oznacza, że \(C=(5;4)\).
Krok 4. Wyznaczenie współrzędnych punktu \(S\).
Punkt \(S\) jest środkiem odcinka \(AC\), zatem korzystając ze wzoru na środek odcinka wyjdzie nam, że:
$$S=\left(\frac{x_{A}+x_{C}}{2};\frac{y_{A}+y_{C}}{2}\right) \\
S=\left(\frac{-4+5}{2};\frac{1+4}{2}\right) \\
S=\left(\frac{1}{2};\frac{5}{2}\right)$$
Krok 5. Obliczenie długości odcinka \(BS\).
Znając współrzędne punktu \(B=(7,-2)\) oraz \(S=\left(\frac{1}{2};\frac{5}{2}\right)\) możemy bez problemu obliczyć poszukiwaną długość odcinka \(BS\):
$$|BS|=\sqrt{(x_{S}-x_{B})^2+(y_{S}-y_{B})^2} \\
|BS|=\sqrt{\left(\frac{1}{2}-7\right)^2+\left(\frac{5}{2}-(-2)\right)^2} \\
|BS|=\sqrt{\left(-6\frac{1}{2}\right)^2+\left(\frac{5}{2}+2\right)^2} \\
|BS|=\sqrt{\left(-\frac{13}{2}\right)^2+\left(\frac{9}{2}\right)^2} \\
|BS|=\sqrt{\frac{169}{4}+\frac{81}{4}} \\
|BS|=\sqrt{\frac{250}{4}} \\
|BS|=\sqrt{\frac{25\cdot10}{4}} \\
|BS|=\frac{5\sqrt{10}}{2}$$