Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Zaznaczając w układzie współrzędnych dane z treści zadania otrzymamy następującą sytuację:
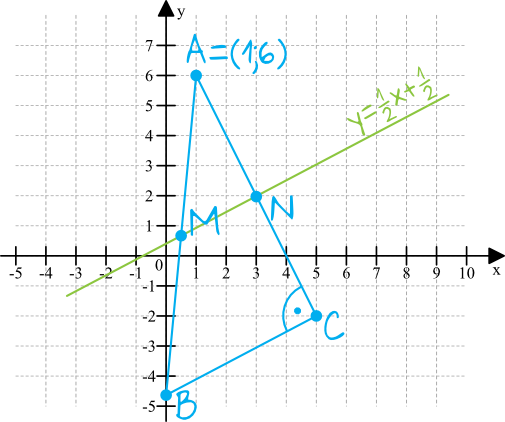
Warto zwrócić uwagę na to, że kąt \(ANM\) będzie także miał miarę \(90°\), bo proste \(BC\) oraz \(MN\) są względem siebie równoległe, zatem miary kątów \(ACB\) oraz \(ANM\) są sobie równe.
Krok 2. Wyznaczenie równania prostej \(AN\) (oraz \(AC\)).
Prosta \(AN\) (lub \(AC\)) to prosta prostopadła do prostej \(y=\frac{1}{2}x+\frac{1}{2}\). Aby dwie proste były względem siebie prostopadłe, to iloczyn ich współczynników kierunkowych musi być równy \(-1\). Skoro nasza pierwsza prosta ma współczynnik \(a=\frac{1}{2}\), to prosta \(AN\) będzie mieć ten współczynnik \(a=-2\), bo \(-2\cdot\frac{1}{2}=-1\). To oznacza, że prosta \(AN\) wyrażać się będzie równaniem \(y=-2x+b\). Do poznania pełnego wzoru musimy jeszcze wyznaczyć współczynnik \(b\).
Współczynnik \(b\) wyznaczymy podstawiając do zapisanego przed chwilą równania wartości współrzędnych jakiegoś punktu, który przez tą prostą przechodzi. W naszym przypadku znamy współrzędne punktu \(A=(1,6)\), zatem podstawiając \(x=1\) oraz \(y=6\) do postaci \(y=-2x+b\) otrzymamy:
$$6=-2\cdot1+b \\
6=-2+b \\
b=8$$
To oznacza, że równanie prostej \(AN\) przyjmuje postać \(y=-2x+8\).
Krok 3. Wyznaczenie współrzędnych punktu \(N\).
Punkt \(N\) jest miejscem przecięcia się prostych \(MN\) oraz \(AN\). Znamy równania jednej i drugiej prostej, zatem tworząc z nich układ równań będziemy mogli wyznaczyć współrzędne punktu \(N\):
$$\begin{cases}
y=\frac{1}{2}x+\frac{1}{2} \\
y=-2x+8
\end{cases}$$
Korzystając z metody podstawiania otrzymamy:
$$\frac{1}{2}x+\frac{1}{2}=-2x+8 \\
2\frac{1}{2}x=7\frac{1}{2} \\
x=3$$
Znamy już wartość współrzędnej iksowej, musimy jeszcze poznać wartość współrzędnej igrekowej, a dokonamy tego podstawiając \(x=3\) do wybranego równania (np. drugiego):
$$y=-2x+8 \\
y=-2\cdot3+8 \\
y=-6+8 \\
y=2$$
To oznacza, że \(N=(3;2)\).
Krok 4. Wyznaczenie współrzędnych punktu \(C\).
Punkt \(N\) jest środkiem odcinka \(AC\). Znamy współrzędne punktu \(A=(1,6)\), znamy też już współrzędne punktu \(N=(3;2)\), zatem możemy ze wzoru na środek odcinka wyznaczyć współrzędne punktu \(C\). Dla przejrzystości obliczeń najlepiej jest oddzielnie policzyć współrzędną iksową i oddzielnie współrzędną igrekową:
$$x_{N}=\frac{x_{A}+x_{C}}{2} \\
3=\frac{1+x_{C}}{2} \\
6=1+x_{C} \\
x_{C}=5 \\
\quad \\
y_{N}=\frac{y_{A}+y_{C}}{2} \\
2=\frac{6+y_{C}}{2} \\
4=6+y_{C} \\
y_{C}=-2$$
Wyszło nam zatem, że \(C=(5;-2)\).
Krok 5. Wyznaczenie równania prostej \(BC\).
Prosta \(BC\) jest równoległa do prostej \(MN\), zatem te dwie proste będą mieć jednakowy współczynnik \(a\). Skoro więc prosta \(MN\) ma współczynnik \(a=\frac{1}{2}\), to i prosta \(BC\) będzie mieć \(a=\frac{1}{2}\). To z kolei oznacza, że prosta \(BC\) będzie wyrażać się równaniem \(y=\frac{1}{2}x+b\). Musimy jeszcze poznać wartość współczynnika \(b\), a dokonamy tego podstawiając do tego równania współrzędne punktu \(C\).
$$-2=\frac{1}{2}\cdot5+b \\
-2=2\frac{1}{2}+b \\
b=-4\frac{1}{2}$$
To oznacza, że równaniem prostej \(BC\) będzie \(y=\frac{1}{2}x-4\frac{1}{2}\).
Krok 6. Wyznaczenie współrzędnych punktu \(B\).
O punkcie \(B\) wiemy tyle, że leży on na osi igreków, czyli na pewno współrzędna iksowa tego punktu jest równa \(x=0\). Możemy więc do równania prostej \(BC\), czyli \(y=\frac{1}{2}x-4\frac{1}{2}\) podstawić \(x=0\) i otrzymamy współrzędną igrekową naszego punktu. Tak prawdę mówiąc, to współrzędną igrekową punktu \(B\) możemy wprost odczytać ze wzoru funkcji - wystarczy spojrzeć na współczynnik \(b\) tej prostej, bo to on pokazuje nam jaka jest współrzędna igrekowa naszego punktu \(B\). Skoro współczynnik \(b=-4\frac{1}{2}\), to współrzędna \(y=-4\frac{1}{2}\). To oznacza, że \(B=\left(0;-4\frac{1}{2}\right)\).