Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Czworościan foremny to bryła mająca wszystkie krawędzie jednakowej długości. Tym samym każda ściana tej bryły jest trójkątem równobocznym. Zaznaczmy na naszym rysunku poszukiwany kąt i zobaczmy jakie odcinki będą go tworzyć:
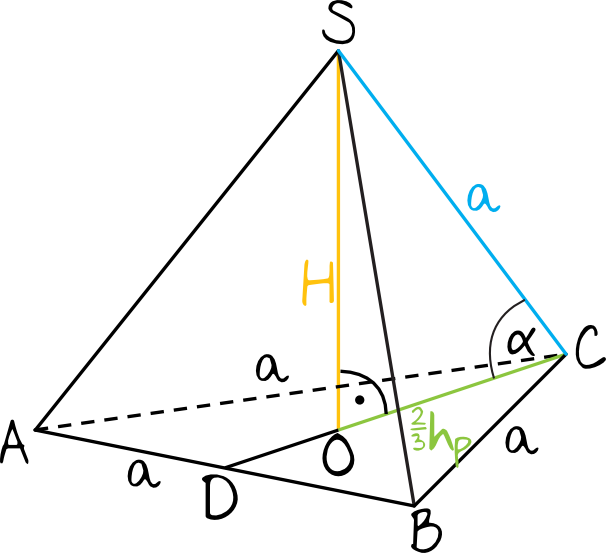
Krok 2. Obliczenie długości odcinka \(OC\).
Spójrzmy na rysunek pomocniczy. Wynika z niego, że odcinek \(OC\) będący dolną przyprostokątną trójkąta prostokątnego ma długość \(\frac{2}{3}h_{p}\). Skoro w podstawie mamy trójkąt równoboczny o boku \(a\), to:
$$|OC|=\frac{2}{3}\cdot h_{p} \\
|OC|=\frac{2}{3}\cdot\frac{a\sqrt{3}}{2} \\
|OC|=\frac{a\sqrt{3}}{3}$$
Krok 3. Obliczenie wartości cosinusa.
Cosinus opisuje nam stosunek długości przyprostokątnej leżącej przy kącie oraz przeciwprostokątnej, zatem:
$$cosα=\frac{|OC|}{|CS|} \\
cosα=\frac{\frac{a\sqrt{3}}{3}}{a} \\
cosα=\frac{a\sqrt{3}}{3}:a \\
cosα=\frac{a\sqrt{3}}{3}\cdot\frac{1}{a} \\
cosα=\frac{\sqrt{3}}{3}$$
Krok 4. Uproszczenie wyrażenia.
Na początek musimy uprościć nasze wyrażenie, korzystając ze wzorów redukcyjnych oraz z jedynki trygonometrycznej. Jeżeli chodzi o wzory redukcyjne to wykorzystamy tutaj zależność \(cos(90°-α)=sinα\). Po lewej stronie równania mamy \(cos^2(90°-α)\), zatem korzystając ze wspomnianego wzoru redukcyjnego możemy zapisać, że to będzie równe \(sin^2α\). Całość wyrażenia będzie więc wyglądać następująco:
$$cos^2(90°-α)-cos2α=sin^2α-cos^2α$$
Z jedynki trygonometrycznej wiemy, że \(sin^2α+cos^2α=1\), czyli że \(sin^2α=1-cos^2α\). Skoro tak, to podstawiając to do wyznaczonej przed chwilą postaci otrzymamy:
$$sin^2α-cos^2α=1-cos^2α-cos^2α=1-2cos^2α$$
Krok 5. Obliczenie wartości całego wyrażenia.
Skoro \(cosα=\frac{\sqrt{3}}{3}\) to wartość naszego wyrażenia będzie równa:
$$1-2cos^2α=1-2\cdot\left(\frac{\sqrt{3}}{3}\right)^2= \\
=1-2\cdot\frac{3}{9}=1-\frac{6}{9}=\frac{3}{9}=\frac{1}{3}$$