W trapezie prostokątnym krótsza przekątna dzieli go na trójkąt prostokątny i trójkąt równoboczny. Dłuższa podstawa trapezu jest równa \(6\). Oblicz obwód tego trapezu.
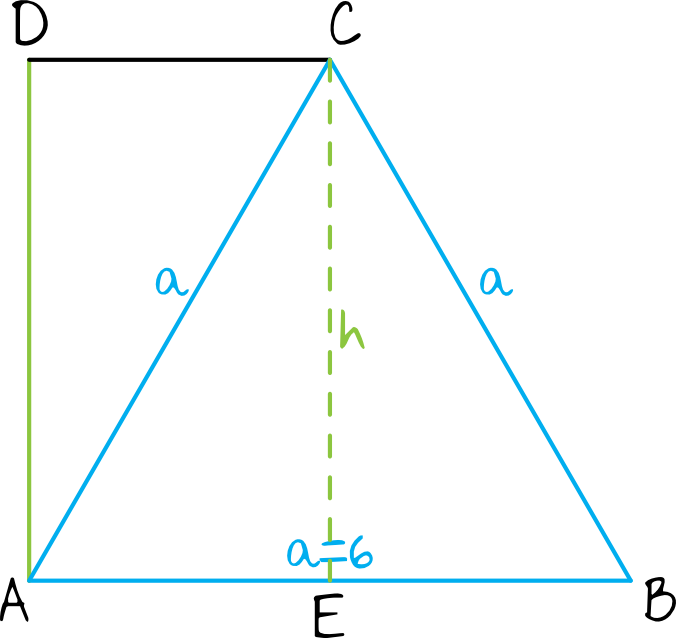
Z rysunku pomocniczego widzimy, że dzięki temu iż przekątna utworzyła nam trójkąt równoboczny to znamy już tak naprawdę trzy długości (z czego dwie przydadzą nam się bezpośrednio do obliczenia obwodu):
$$|AB|=|AC|=|BC|=6$$
Pozostaje nam do rozstrzygnięcia jaka jest długość boku \(DA\) oraz \(DC\).
Długość tego boku jest identyczna co wysokość naszego trójkąta równoramiennego, czyli \(|DA|=|CE|\). Znając długość boku trójkąta równobocznego możemy szybko obliczyć wysokość figury.
$$|DA|=h=\frac{a\sqrt{3}}{2}=\frac{6\sqrt{3}}{2}=3\sqrt{3}$$
Długość boku \(DC\) możemy obliczyć tak naprawdę na dwa sposoby. Jeśli pamiętamy, że wysokość trójkąta równobocznego dzieli podstawę na dwie równe części, to po wyprowadzeniu wysokości z wierzchołka \(C\) otrzymamy bok \(AE\), którego długość jest równa \(3\) (patrz rysunek). Analogicznie więc bok \(DC\) ma długość \(3\).
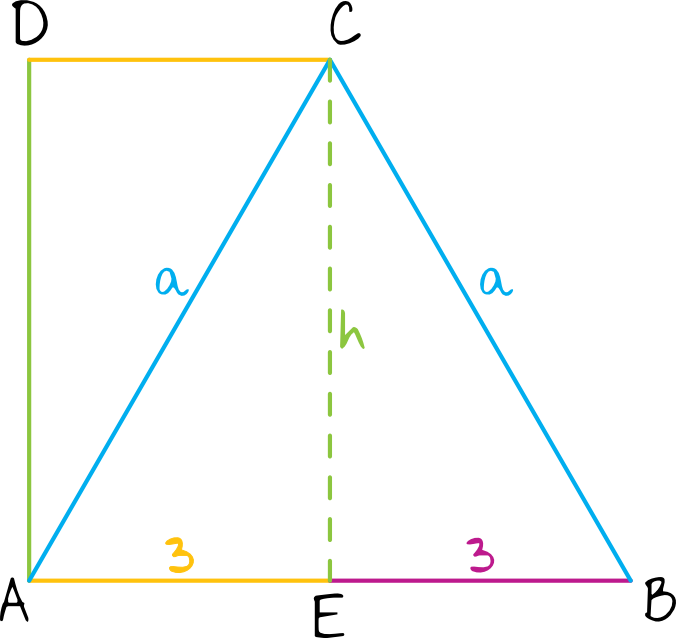
Jeśli nie widzimy tej zależności, to możemy obliczyć długość boku \(DC\) z Twierdzenia Pitagorasa, bo długość \(DA\) i \(CA\) jest nam przecież znana.
$$a^2+b^2=c^2 \\
|DC|^2+|DA|^2=|CA|^2 \\
|DC|^2+(3\sqrt{3})^2=6^2 \\
|DC|^2+(9\cdot3)=36 \\
|DC|^2+27=36 \\
|DC|^2=9 \\
|DC|=3 \quad\lor\quad |DC|=-3$$
(wartość ujemną oczywiście odrzucamy)
Znamy już wszystkie potrzebne miary, więc bez problemu obliczymy długość naszego obwodu:
$$Obw=6+6+3+3\sqrt{3}=15+3\sqrt{3}$$
Obwód trapezu jest równy \(15+3\sqrt{3}\).


Możnaby obliczyć wysokość z Pitagorasa?
Pewnie :) Jak dostrzeżemy że |DC|=3 oraz |AB|=6, to faktycznie można odcinek |AD| obliczyć z Twierdzenia Pitagorasa.
dzień dobry czy 3 pierwiastki z trzech można zapisać jako 3 ? i wtedy obwód liczyć 3+3+6+6=?
Ale 3√3 to nie jest 3 ;) Zobacz, √3 to coś około 1,7 zatem 3√3 to jest ponad 5 ;)