W trapezie \(KLMN\), w którym \(KL||MN\), kąt \(LKN\) jest prosty (zobacz rysunek) oraz dane są: \(|MN|=3\), \(|KN|=4\sqrt{3}\), \(|\sphericalangle KLM|=60°\). Pole tego trapezu jest równe:

\(4+2\sqrt{3}\)
\(10\sqrt{3}\)
\(20\sqrt{3}\)
\(24+6\sqrt{3}\)
Rozwiązanie:
Krok 1. Obliczenie długości podstawy \(KL\).
Do obliczenia pola trapezu brakuje nam tylko znajomości długości dolnej podstawy. Sporządźmy sobie prosty rysunek:
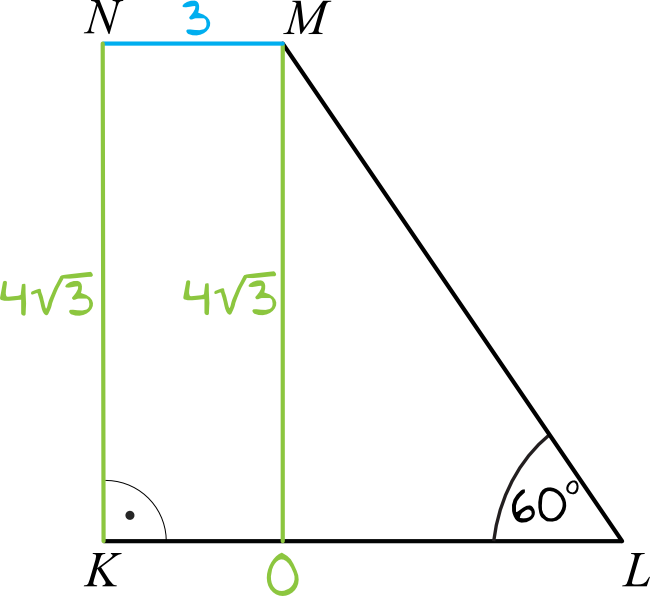
Na podstawie tego szkicu widzimy, że: \(|NM|=|KO|=3\) oraz \(|NK|=|MO|=4\sqrt{3}\). Jeśli obliczymy długość odcinka \(|OL|\) (a możemy to zrobić korzystając z tangensa) to poznamy także długość dolnej podstawy trapezu.
$$tgα=\frac{|MO|}{|OL|} \\
\sqrt{3}=\frac{4\sqrt{3}}{|OL|} \\
\sqrt{3}\cdot|OL|=4\sqrt{3} \\
|OL|=\frac{4\sqrt{3}}{\sqrt{3}} \\
|OL|=4$$
Stąd też \(|KL|=|KO|+|OL|=3+4=7\).
Krok 2. Obliczenie pola trapezu.
$$P=\frac{1}{2}(a+b)\cdot h \\
P=\frac{1}{2}(7+3)\cdot4\sqrt{3} \\
P=5\cdot4\sqrt{3} \\
P=20\sqrt{3}$$
Odpowiedź:
C. \(20\sqrt{3}\)


Dziękuje,bardzo uczę chłopaka matematyki i w końcu coś rozumie ! Pozdrawiam !!!
I to mi się podoba! :) Trzymam za Was kciuki i pozdrawiam serdecznie!
Fajna ta stronka,uczę się sama i często z niej korzystam.
Matematyka mnie wycisza i uspokaja môj umysł.
Fajnie gdyby były tu sprawdzianý i rôżnego rodzaju zadania powtórzeniowe do wydruku na ćwiczenia nawet odpłatnie bym kupiła bo samemu zadaņ wyszukiwanie to męczarnia