W trapezie \(ABCD\) o podstawach \(AB\) i \(CD\) przekątne \(AC\) oraz \(BD\) przecinają się w punkcie \(S\). Wykaż, że jeżeli \(|AS|=\frac{5}{6}|AC|\), to pole trójkąta \(ABS\) jest \(25\) razy większe od pola trójkąta \(DCS\).
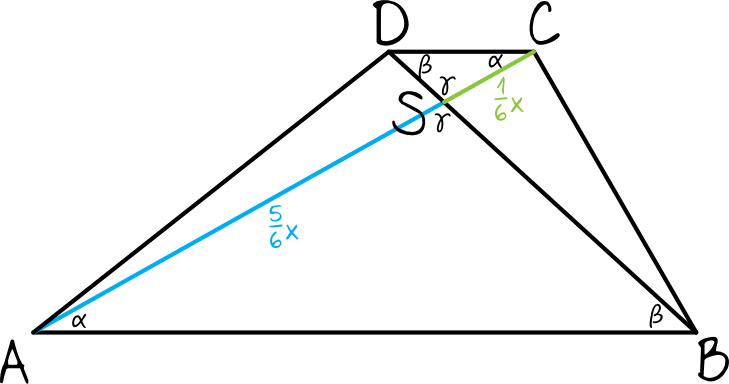
Pierwszą rzeczą, którą musimy zauważyć to fakt iż trójkąty \(ABS\) oraz \(DCS\) są podobne na mocy cechy kąt-kąt-kąt. Wynika to z zależności między kątami wierzchołkowymi i naprzemianległymi. Jeśli \(|\sphericalangle SAB|=α\) to kąt naprzemianległy \(|\sphericalangle SCD|=α\). Analogicznie \(|\sphericalangle ABS|=|\sphericalangle SDC|=β\). Natomiast \(|\sphericalangle ASB|=|\sphericalangle DSC|=γ\) bo są to kąty wierzchołkowe.
Jeżeli długość przekątnej \(AC\) oznaczymy sobie jako \(x\), to odcinek \(|AS|=\frac{5}{6}x\) oraz \(|SC|=\frac{1}{6}x\) (wynika to wprost z treści zadania). Zatem skala podobieństw tych trójkątów jest równa:
$$k=\frac{|AS|}{|SC|}=\frac{\frac{5}{6}}{\frac{1}{6}}=5$$
Jeżeli skala podobieństwa dwóch figur jest równa \(k\), to stosunek pól powierzchni tych dwóch figur jest równy \(k^2\). Skoro w naszym przypadku \(k=5\), to \(k^2=25\). Pole trójkąta \(ABS\) jest więc \(25\) razy większe od pola trójkąta \(DCS\) i właśnie w ten sposób możemy zakończyć nasze dowodzenie.
Udowodniono na podstawie podobieństw trójkątów.


Dziękuję !