Rozwiązanie
Krok 1. Obliczenie długości boków prostokąta.
Wprowadźmy do zadania następujące obliczenia:
\(x\) - długość prostokąta
\(x-2\) szerokość prostokąta
Skoro obwód tej figury jest równy \(28\), to:
$$2\cdot+2\cdot(x-2)=28 \\
2x+2x-4=28 \\
4x-4=28 \\
4x=32 \\
x=8$$
W ten sposób obliczyliśmy długość prostokąta, a zatem jego szerokość wyniesie:
$$8-2=6$$
To oznacza, że jest to prostokąt o wymiarach \(8cm\times6cm\).
Krok 2. Rozwiązanie pierwszej części zadania.
Sytuacja z treści zadania wygląda następująco:
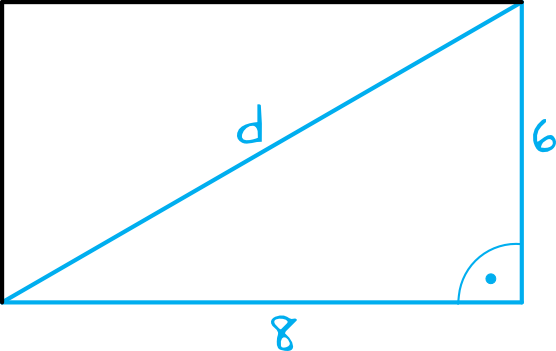
Boki prostokąta oraz przekątna tworzą trójkąt prostokątny, zatem poszukiwaną długość przekątnej możemy wyznaczyć z Twierdzenia Pitagorasa:
$$6^2+8^2=d^2 \\
36+64=d^2 \\
d^2=100 \\
d=10 \quad\lor\quad d=-10$$
Oczywiście ujemny wynik nas nie interesuje, bo długość przekątnej musi być dodania, zatem zostaje nam \(d=10cm\).
Krok 3. Rozwiązanie drugiej części zadania.
Szerokość prostokąta jest równa \(6cm\), długość to \(8cm\), zatem szerokość stanowi:
$$\frac{6cm}{8cm}=\frac{3}{4}$$