Rozwiązanie
Krok 1. Dostrzeżenie trójkątów równoramiennych.
Z własności stycznych do okręgu wynika, że odcinki \(AC\) oraz \(BC\) mają jednakową miarę, a skoro tak, to trójkąt \(ACB\) jest równoramienny.
Równoramienny będzie także trójkąt \(ASD\), ponieważ odcinki \(SA\) oraz \(SD\) są promieniami okręgu.
Krok 2. Sporządzenie rysunku pomocniczego.
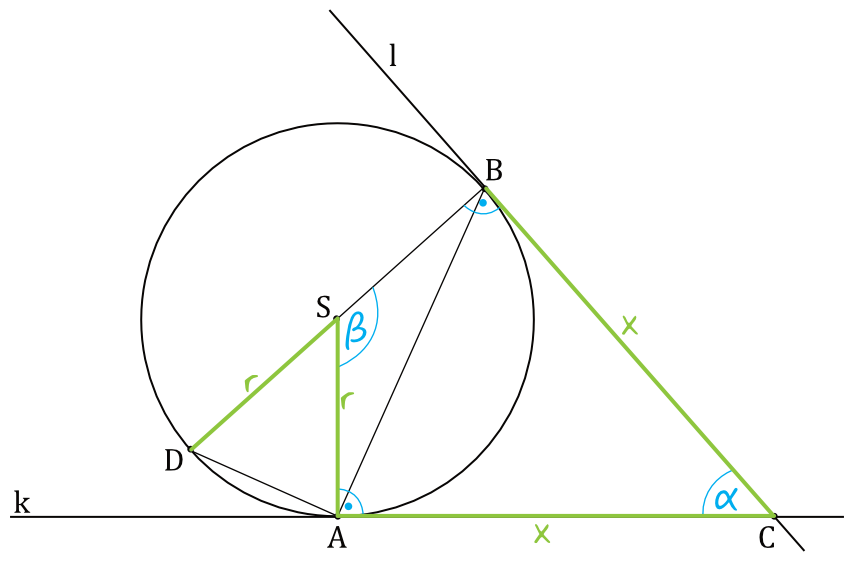
Oznaczmy kąt \(ACB\) jako \(\alpha\) i spójrzmy na czworokąt \(ACBS\). W tym czworokącie mamy nasz kąt alfa oraz dwa kąty proste (kąty \(SAC\) oraz \(SBC\) muszą być proste, bo styczna tworzy z promieniem okręgu zawsze kąt prosty). Suma miar kątów czworokąta jest równa \(360°\), a skoro tak, to kąt \(ASB\) ma miarę:
$$\beta=360°-90°-90°-\alpha \\
\beta=180°-\alpha$$
Krok 3. Wyznaczenie miary kąta \(\alpha\).
Kąt \(DSA\) jest kątem przyległym do naszego kąta \(\beta\). Suma miar kątów przyległych jest równa \(180°\), a skoro tak, to:
$$|\sphericalangle DSA|=180°-\beta \\
|\sphericalangle DSA|=180°-(180°-\alpha) \\
|\sphericalangle DSA|=180°-180°+\alpha \\
|\sphericalangle DSA|=\alpha$$
Krok 4. Zakończenie dowodzenia.
Z własności trójkątów równoramiennych wiemy, że kąty przy podstawie mają jednakową miarę. Spójrzmy zatem najpierw na trójkąt \(ABC\). Tutaj podstawą trójkąta jest bok \(AB\), więc możemy zapisać, że kąty przy tej podstawie mają jednakową miarę, niech to będzie \(\gamma\). Możemy sobie nawet zapisać, że miara takiego kąta \(\gamma\) będzie równa \(\frac{180°-\alpha}{2}\).
Analogiczna sytuacja jest w trójkącie \(ASD\). Tutaj podstawą trójkąta jest bok \(AD\) i to tutaj także kąty przy podstawie będą miały jednakową miarę. Skoro kąt między ramionami tego trójkąta to \(\alpha\) (czyli identycznie jak w trójkącie \(ABC\)), to tutaj także kąty przy podstawie będą miały miarę równą \(\gamma\).
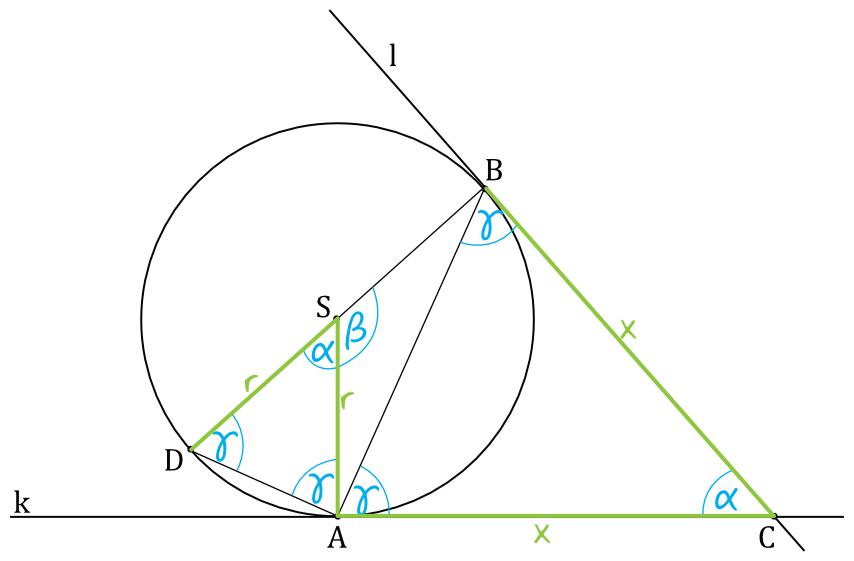
W ten sposób udowodniliśmy, że kąty w trójkątach \(ABC\) oraz \(ASD\) są jednakowej miary, a to oznacza, że te trójkąty są podobne na podstawie cechy kąt-kąt-kąt.