Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Nanosząc na rysunek kluczowe informacje, otrzymamy taką oto sytuację:
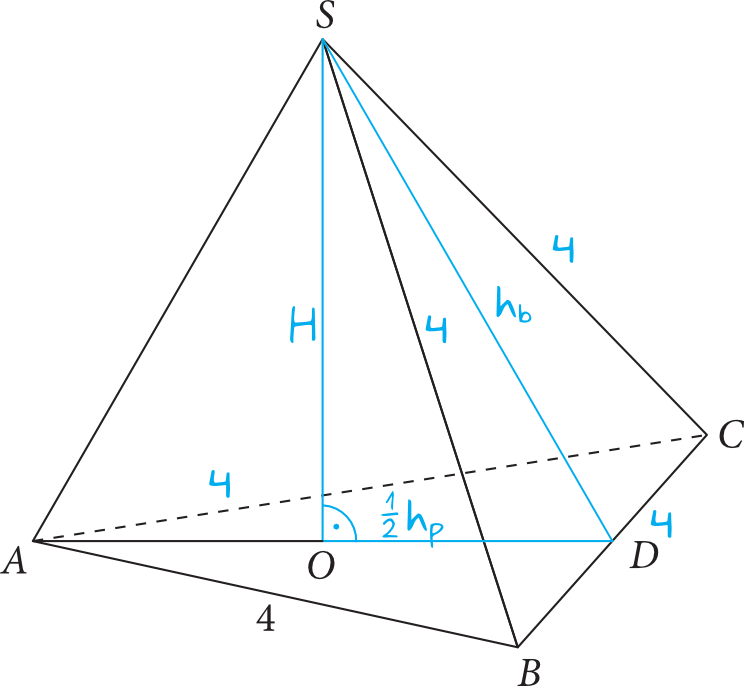
Krok 2. Obliczenie wysokości trójkąta znajdującego się w podstawie.
W podstawie mamy trójkąt równoboczny o boku \(a=4\). Korzystając ze wzoru na wysokość trójkąta równobocznego możemy zapisać, że:
$$h_{p}=\frac{a\sqrt{3}}{2} \\
h_{p}=\frac{4\sqrt{3}}{2} \\
h_{p}=2\sqrt{3}$$
Krok 3. Obliczenie długości odcinka \(OD\).
Wysokość ostrosłupa \(SO\) dzieli nam wysokość podstawy na dwie równe części (tak wynika wprost z zadania). Każda z tych części ma długość \(\frac{1}{2}h_{p}\). Skoro tak, to odcinek \(OD\) będzie mieć długość:
$$|OD|=\frac{1}{2}\cdot2\sqrt{3} \\
|OD|=\sqrt{3}$$
Krok 4. Obliczenie wysokości trójkąta \(BCS\).
Trójkąt \(BCS\) jest także trójkątem równobocznym o boku \(a=4\) (wynika to z zadania). Jego wysokość obliczymy więc dokładnie tak samo, jak wysokość \(h_{p}\), zatem:
$$h_{b}=\frac{a\sqrt{3}}{2} \\
h_{b}=\frac{4\sqrt{3}}{2} \\
h_{b}=2\sqrt{3}$$
Krok 5. Obliczenie wysokości ostrosłupa.
Spoglądamy teraz na kluczowy trójkąt prostokątny \(SOD\). Korzystając z Twierdzenia Pitagorasa możemy obliczyć wysokość ostrosłupa:
$$(\sqrt{3})^2+H^2=(2\sqrt{3})^2 \\
3+H^2=4\cdot3 \\
3+H^2=12 \\
H^2=9 \\
H=3 \quad\lor\quad H=-3$$
Ujemną wartość oczywiście odrzucamy, zatem zostaje nam \(H=3\).
Krok 6. Obliczenie pola powierzchni podstawy.
W podstawie mamy trójkąt równoboczny o boku \(a=4\). Korzystając ze wzoru na pole trójkąta równobocznego możemy zapisać, że:
$$P_{p}=\frac{a^2\sqrt{3}}{4} \\
P_{p}=\frac{4^2\sqrt{3}}{4} \\
P_{p}=\frac{16\sqrt{3}}{4} \\
P_{p}=4\sqrt{3}$$
Krok 7. Obliczenie objętości ostrosłupa.
Wiemy, że \(P_{p}=4\sqrt{3}\). Wysokość ostrosłupa też już znamy, bowiem \(H=3\). Możemy zatem przystąpić do obliczenia objętości:
$$V=\frac{1}{3}P_{p}\cdot H \\
V=\frac{1}{3}\cdot4\sqrt{3}\cdot3 \\
V=4\sqrt{3}$$
Krok 8. Obliczenie długości krawędzi \(AS\).
Spoglądamy tym razem na trójkąt prostokątny \(AOS\). Odcinek \(AO\) będzie taki sam jak \(OD\), czyli ma długość \(|AS|=\sqrt{3}\). Wiemy też, że wysokość ostrosłupa jest równa \(H=3\), zatem ponownie możemy skorzystać z Twierdzenia Pitagorasa i zapisać, że:
$$(\sqrt{3})^2+3^2=|AS|^2 \\
3+9=|AS|^2 \\
|AS|^2=12 \\
|AS|=\sqrt{12}=\sqrt{4\cdot3}=2\sqrt{3}$$
Krok 9. Obliczenie pola powierzchni trójkąta \(ABS\) (oraz \(ACS\)).
Trójkąt \(ABS\) jest trójkątem równoramiennym (takim obróconym), w którym podstawa \(|AS|=2\sqrt{3}\), a ramiona \(|AB|=4\) oraz \(|BS|=4\).
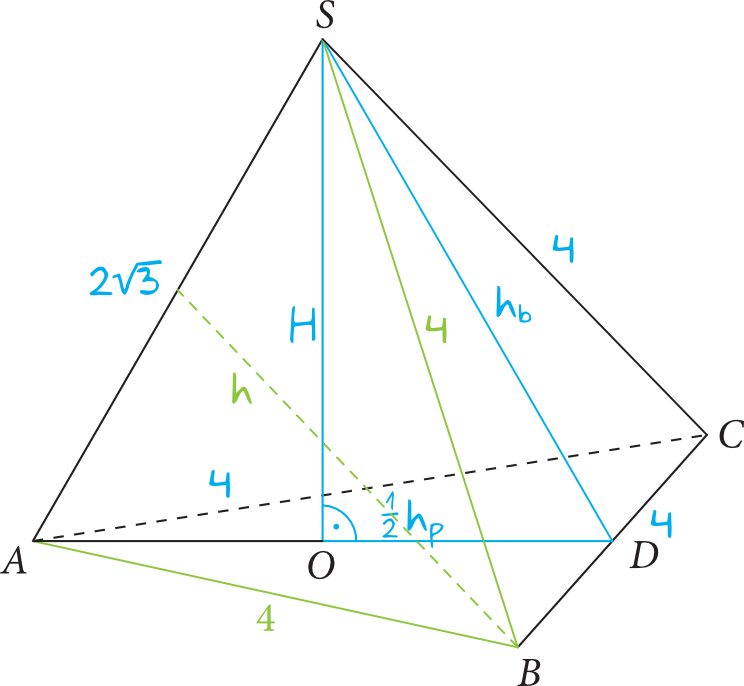
Musimy poznać pole tego trójkąta, a do tego potrzebujemy wysokości. Wiemy, że w trójkątach równoramiennych wysokość dzieli podstawę na dwie równe części (patrz rysunek), tworząc nam tym samym kolejne trójkąty prostokątne. Ponownie z pomocą przyjdzie nam więc Twierdzenie Pitagorasa:
$$(\sqrt{3})^2+h^2=4^2 \\
3+h^2=16 \\
h=\sqrt{13}$$
To oznacza, że pole trójkąta \(ABS\) będzie równe:
$$P_{ABS}=\frac{1}{2}\cdot2\sqrt{3}\cdot\sqrt{13} \\
P_{ABS}=\sqrt{3}\cdot\sqrt{13} \\
P_{ABS}=\sqrt{39}$$
Analogiczna sytuacja jest w trójkącie \(ACS\) (tutaj także mamy podstawę \(|AS|=2\sqrt{3}\) oraz ramiona \(|AC|=4\) oraz \(|CS|=4\)), zatem także \(P_{ACS}=\sqrt{39}\).
Krok 10. Obliczenie pola powierzchni całkowitej.
Podsumowując - nasz trójkąt składa się z dwóch trójkątów równobocznych o polu \(4\sqrt{3}\) (wyliczyliśmy to w szóstym kroku) oraz dwóch trójkątów o polu \(\sqrt{39}\) (wyliczyliśmy to w dziewiątym kroku). Skoro tak, to pole powierzchni całkowitej będzie równe:
$$P_{c}=4\sqrt{3}+4\sqrt{3}+\sqrt{39}+\sqrt{39}=8\sqrt{3}+2\sqrt{39}$$