Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Narysujmy wskazany ostrosłup, nanosząc na niego dane z treści zadania (w szczególności kąt nachylenia ściany bocznej do płaszczyzny podstawy). Warto tutaj od razu pamiętać, że skoro ostrosłup jest prawidłowy czworokątny, to w podstawie będziemy mieć kwadrat.
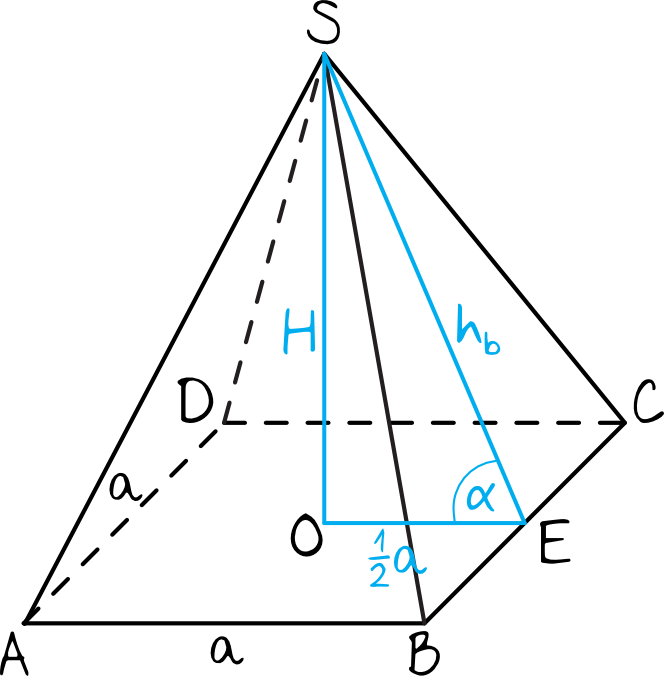
Krok 2. Zapisanie zależności między wysokością ściany bocznej i krawędzią podstawy.
Spójrzmy na trójkąt prostokątny \(OES\). Dolna przyprostokątna ma długość \(\frac{1}{2}a\), natomiast przeciwprostokątna to wysokość ściany bocznej. Stosunek długości tych dwóch boków opisuje nam właśnie cosinus kąta \(α\), który jest równy \(\frac{1}{3}\). Możemy więc zapisać, że:
$$cosα=\frac{\frac{1}{2}a}{h_{b}} \\
\frac{1}{3}=\frac{\frac{1}{2}a}{h_{b}} \quad\bigg/\cdot h_{b} \\
\frac{1}{3}h_{b}=\frac{1}{2}a \quad\bigg/\cdot3 \\
h_{b}=\frac{3}{2}a$$
Krok 3. Wyznaczenie długości krawędzi podstawy.
W ścianie bocznej mamy trójkąt o podstawie \(a\) oraz wysokości \(h_{b}\), która ja już ustaliliśmy jest równa \(\frac{3}{2}a\). Skoro pole tego trójkąta jest równe \(12\), to:
$$P=\frac{1}{2}\cdot a\cdot h_{b} \\
12=\frac{1}{2}\cdot a\cdot\frac{3}{2}a \\
12=\frac{3}{4}a^2 \quad\bigg/\cdot\frac{4}{3} \\
a^2=16 \\
a=4 \quad\lor\quad a=-4$$
Długość boku nie może być ujemna, zatem zostaje nam \(a=4\).
Krok 4. Wyznaczenie długości wysokości ściany bocznej.
Wiemy już, że \(h_{b}=\frac{3}{2}\). Skoro więc \(a=4\), to:
$$h_{b}=\frac{3}{2}\cdot4 \\
h_{b}=6$$
Krok 5. Obliczenie wysokości ostrosłupa.
Spójrzmy ponownie na trójkąt \(OES\). Odcinek \(AB\) ma długość \(\frac{1}{2}a\), czyli \(|AB|=2\). Wiemy też, że przeciwprostokątna tego trójkąta ma długość równą \(6\). W związku z tym korzystając z Twierdzenia Pitagorasa możemy wyznaczyć brakującą wysokość całego ostrosłupa:
$$2^2+H^2=6^2 \\
4+H^2=36 \\
H^2=32 \\
H=\sqrt{32} \quad\lor\quad H=-\sqrt{32}$$
Ujemną wartość oczywiście odrzucamy, bo wysokość musi być dodatnia. To oznacza, że \(H=\sqrt{32}\), co po wyłączeniu czynnika przed znak pierwiastka możemy jeszcze zapisać jako \(H=\sqrt{16\cdot2}=4\sqrt{2}\).
Krok 6. Obliczenie objętości ostrosłupa.
Mając długość krawędzi podstawy \(a=4\) oraz wysokość bryły \(H=4\sqrt{2}\) możemy bez przeszkód obliczyć objętość ostrosłupa:
$$V=\frac{1}{3}P_{p}\cdot H \\
V=\frac{1}{3}a^2\cdot H \\
V=\frac{1}{3}\cdot4^2\cdot4\sqrt{2} \\
V=\frac{1}{3}\cdot16\cdot4\sqrt{2} \\
V=21\frac{1}{3}\sqrt{2}$$