Dany jest okrąg o środku \(S=(-6,-8)\) i promieniu \(2014\). Obrazem tego okręgu w symetrii osiowej względem osi \(Oy\) jest okrąg o środku w punkcie \(S_{1}\). Odległość między punktami \(S\) i \(S_{1}\) jest równa:
\(12\)
\(16\)
\(2014\)
\(4028\)
Rozwiązanie:
Spróbujmy narysować sobie szkic tej sytuacji, całość będzie wyglądać następująco:
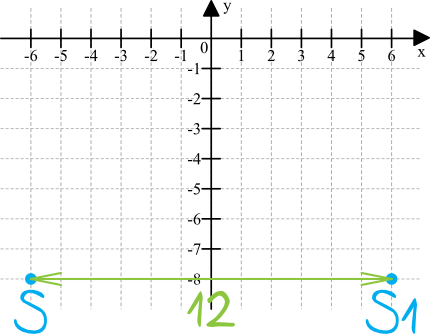
Z rysunku widać, że kompletnie nie interesuje nas promień okręgu, dlatego zupełnie nie ma co się przejmować tak dużymi liczbami. My musimy skupić się tylko na środkach okręgów. Odległość między środkami okręgów jest równa \(6+6=12\) jednostek.
Odpowiedź:
A. \(12\)


Dlaczego jak jest w poleceniu: Obrazem tego okręgu w symetrii osiowej względem osi Oy to tak naprawdę patrzymy na oś X coś źle rozumiem ewidentnie proszę o pomoc
Symetria względem osi Oy wygląda mniej więcej tak, jakbyś postawił/a lustro na osi igreków :) Ten punkt przeskoczy nam więc właśnie przez oś igreków na drugą stronę. Z tego też względu charakterystyczne dla takiej symetrii jest to, że punkt poddany symetrii nie zmieni współrzędnej igrekowej (bo będzie na tej samej wysokości), ale zmieni współrzędną iksową (bo „przeskoczy”).
No i właśnie dlatego interesują nas tutaj te współrzędne iksowe, bo dzięki nim obliczymy odległość między tymi dwoma punktami.
już rozumiem, dziękuje bardzo za pomoc, miłego wieczoru!
Cieszę się, że mogłem pomóc :) Pozdrawiam!
Próbowałam to obliczyć ze wzoru na długość odcinka z dwóch punktów (tego pod pierwiastkiem) dlaczego wyszedł mi zły wynik? Tak nie można było tego zrobić?
Można tym wzorem :) A dlaczego Ci nie wyszło, to hmmm, podejrzewam, że pogubiłaś się w znakach. Obliczenia powinny wyglądać następująco:
√(-6-6)^2+(8-8)^2
√(-12)^2+0^2
√144
12
Dlaczego nie możemy pomnożyć promienia razy 2 jak odległość miedzy tymi środkami to odległość dwóch promieni?
Odległość między środkami okręgów nie zależy od długości promienia ;) Może być mały okrąg, może być duży, a jak mają środki w tych samych miejscach to odległość będzie taka sama ;)