Rozwiązanie
Krok 1. Wyznaczenie miary kąta \(BSD\).
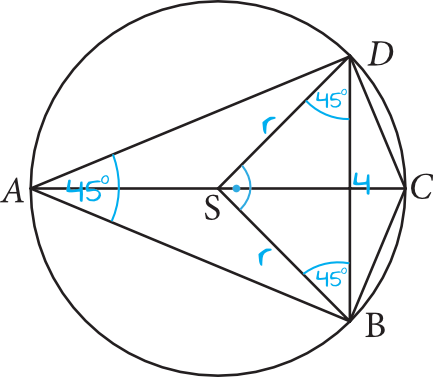
Spójrzmy na kąty \(BAD\) oraz \(BSD\). Są to kąty oparte na tym samym łuku. Kąt \(BAD\) jest kątem wpisanym i znamy jego miarę, jest ona równa \(45°\). Kąt \(BSD\) jest kątem środkowym, zatem zgodnie z własnościami kątów środkowych i wpisanych (opartych na tym samym łuku) jego miara będzie dwa razy większa, czyli:
$$|\sphericalangle BSD|=2\cdot45° \\
|\sphericalangle BSD|=90°$$
Krok 2. Obliczenie długości promienia okręgu.
Spójrzmy na trójkąt \(SBD\). Udowodniliśmy przed chwilą, że jest to trójkąt prostokątny. Jego przyprostokątne są tak naprawdę długościami promienia okręgu, czyli będzie to trójkąt prostokątny równoramienny. Można nawet powiedzieć, że to jest taka połówka kwadratu. Z własności kwadratów oraz trójkątów o kątach \(45°,45°,90°\) (a ten trójkąt właśnie takim będzie) wiemy, że kwadrat o boku \(r\) ma przekątną o długości \(r\sqrt{2}\). My wiemy, że bok \(BD\) ma długość \(4\), zatem:
$$r\sqrt{2}=4 \\
r=\frac{4}{\sqrt{2}} \\
r=\frac{4\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}} \\
r=\frac{4\sqrt{2}}{2} \\
r=2\sqrt{2}$$
Wyszło nam więc, że boki \(SB\) oraz \(SD\) mają długość \(2\sqrt{2}\), czyli promienie naszego okręgu mają długość \(r=2\sqrt{2}\).
Krok 3. Obliczenie długości dłuższej przekątnej deltoidu.
Dłuższa przekątna deltoidu jest średnicą okręgu. Skoro więc promień ma długość \(r=2\sqrt{2}\), to:
$$|AC|=2r \\
|AC|=2\cdot2\sqrt{2} \\
|AC|=4\sqrt{2}$$
Krok 4. Obliczenie pola powierzchni deltoidu.
Wiemy już, że przekątne deltoidu mają długości \(4\sqrt{2}\) oraz \(4\), zatem:
$$P=\frac{1}{2}ef \\
P=\frac{1}{2}\cdot4\sqrt{2}\cdot4 \\
P=2\sqrt{2}\cdot4 \\
P=8\sqrt{2}$$