Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Aby ocenić prawdziwość obydwu zdań najprościej będzie sporządzić rysunek pomocniczy, na którym zamieścimy informacje z treści zadania:
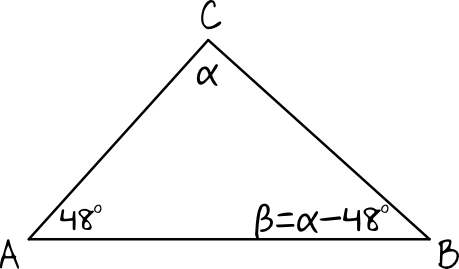
Krok 2. Ocena prawdziwości pierwszego zdania.
Na podstawie rysunku spróbujmy obliczyć miary poszczególnych kątów. Wiedząc, że suma miar kątów w trójkącie jest równa \(180°\) możemy zapisać, że:
$$48°+α+β=180° \\
48°+α+α-48°=180° \\
2α=180° \\
α=90°$$
W pierwszym pytaniu mamy stwierdzić jaka jest miara kąta przy wierzchołku \(B\), a będzie ona równa zgodnie z rysunkiem:
$$β=α-48° \\
β=90°-48° \\
β=42°$$
Pierwsze zdanie jest więc fałszem.
Krok 3. Ocena prawdziwości drugiego zdania.
W obliczeń wykonanych w drugim kroku wyszło nam, że kąt przy wierzchołku \(C\) ma miarę \(90°\), zatem prawdą jest, że ten trójkąt jest prostokątny.