Rozwiązanie
Ustalmy może o co dokładnie chodzi w tym zadaniu. Jeżeli funkcja nie ma miejsc zerowych, to tak obrazowo rzecz ujmując, podczas wyznaczania miejsc zerowych musiała nam wyjść ujemna delta. Wykresy takich funkcji wyglądają w ten sposób, że cała parabola jest albo nad osią iksów, albo też pod nią. Wszystko objaśni poniższy rysunek:
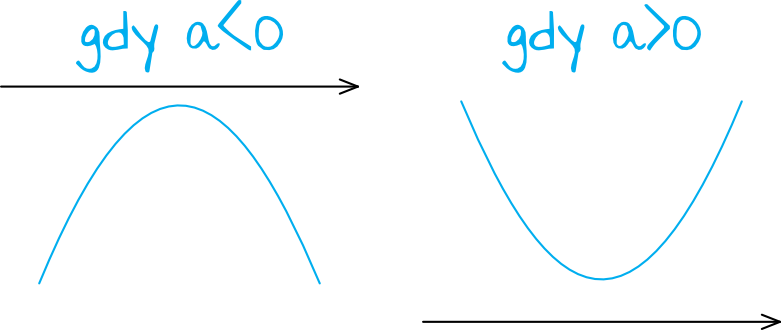
Celem zadania jest ustalenie który z tych wariantów ma tutaj miejsce. Już ustaliliśmy, że delta musi być ujemna, czyli że \(b^2-4ac\lt0\). Co się musi stać, by ta delta była ujemna? Jak się dobrze przyjrzymy, to zauważymy, że \(b^2\) zawsze jest liczbą nieujemną, więc aby delta wyszła ujemna, to \(4ac\), musi być jeszcze większe od tego \(b^2\). Wniosek z tego taki, że \(4ac\) musi być liczbą dodatnią.
W treści zadania mamy informację, że \(c\) jest liczbą ujemną, a skoro \(4ac\) musi wyjść dodatnie, to tym samym współczynnik \(a\) także musi być ujemny. Jeżeli współczynnik \(a\) jest ujemny, to ramiona paraboli są skierowane do dołu, zatem aby ta parabola nie przecinała osi \(Ox\), to musi się w całości znaleźć pod tą osią. Stąd też odpowiedź brzmi, że wykres tej funkcji leży pod osią \(Ox\), ponieważ \(a\lt0\) oraz \(b^2-4ac\lt0\).