Przed Tobą sprawdzian z matematyki, który sprawdzi Twoją wiedzę z działu: Wielkości wprost i odwrotnie proporcjonalne. W teście znajduje się 10 zadań, a każde z nich jest warte 1 punkt. Całość powinna Ci zająć około 15 minut. Po zakończeniu sprawdzianu możesz przejrzeć swoje odpowiedzi wraz z pełnymi rozwiązaniami do zadań. Życzę powodzenia!
Zadanie 1. (1pkt) Pociąg pokonał trasę \(220km\) w ciągu \(4\) godzin. Jaką trasę pokona ten pociąg w \(5\) godzin, jeżeli utrzyma on na trasie swoją dotychczasową średnią prędkość?
Zadanie 2. (1pkt) Samochód pokonał daną trasę jadąc ze średnią prędkością \(v=90\frac{km}{h}\) przez \(3\) godziny. Z jaką prędkością trzeba byłoby jechać, aby tą samą trasę pokonać w \(2\) godziny i \(30\) minut?
Zadanie 3. (1pkt) Do ulepienia \(80\) pierogów zużyto \(0,5kg\) mąki. Ile mąki trzeba zużyć do zrobienia \(100\) pierogów?
Zadanie 4. (1pkt) Dwóch pracowników jest w stanie wyłożyć kostkę brukową w ciągu \(18\) dni. Ilu dodatkowych pracowników trzeba byłoby zatrudnić, aby kostka została ułożona w \(4\) dni, zakładając że każdy pracuje tak samo efektywnie?
Zadanie 5. (1pkt) Dana jest funkcja \(f(x)=\frac{2}{x}\). Która z tych wartości jest największa?
Zadanie 6. (1pkt) Dana jest funkcja \(f(x)=\frac{-4}{x}+1\). Dziedziną tej funkcji jest \(x\in\mathbb{R}\backslash\{0\}\).
Zadanie 7. (1pkt) Funkcja \(f(x)=\frac{-4}{x}\) przechodzi przez punkt \(A=\left(-\frac{1}{2};2\right)\).
Zadanie 8. (1pkt) 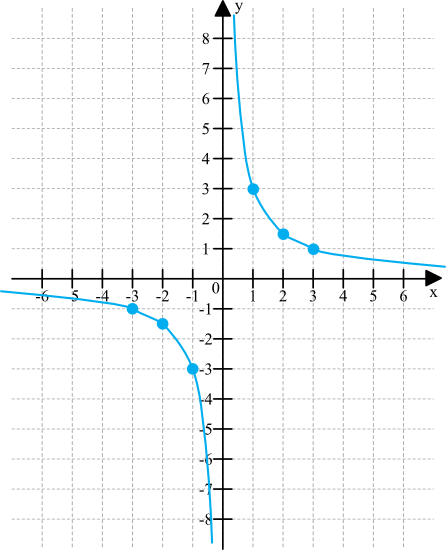
Jaś twierdzi, że powyższa funkcja jest malejąca tylko w przedziale \((-\infty;0)\). Małgosia uważa, że ta funkcja jest malejąca w przedziałach \((-\infty;0)\) oraz \((0;+\infty)\). Kto ma rację?
Zadanie 9. (1pkt) Do przewiezienia piasku na budowę potrzeba \(6\) kursów ciężarówki o ładowności \(5\) ton. Ile kursów trzeba byłoby zrobić, gdyby ładowność ciężarówki wynosiła \(8\) ton?
Zadanie 10. (1pkt) 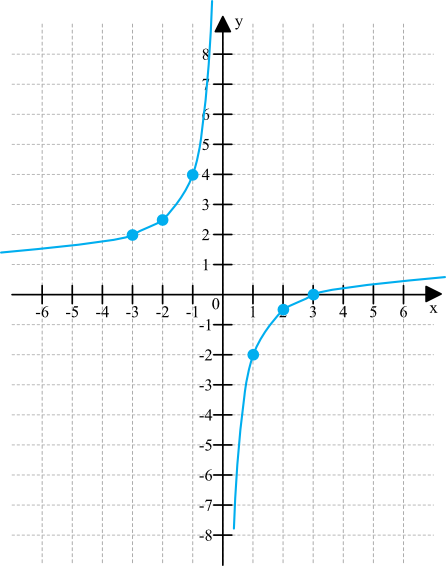
Wzorem powyższej funkcji jest:
