Trójkąt prostokątny o przyprostokątnych \(4\) i \(6\) obracamy wokół dłuższej przyprostokątnej. Objętość powstałego stożka jest równa:
\(96π\)
\(48π\)
\(32π\)
\(8π\)
Rozwiązanie:
Dobrze jest sobie zwizualizować tę sytuację prostym rysunkiem:
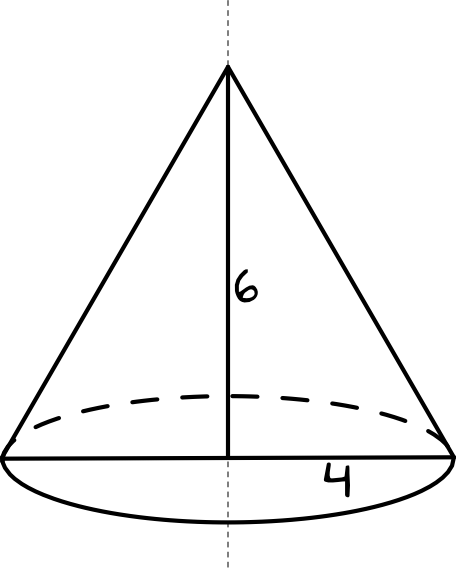
Teraz widzimy, że promień podstawy jest równy \(r=4\), natomiast wysokość stożka jest równa \(H=6\). To oznacza, że objętość tej bryły będzie równa:
$$V=\frac{1}{3}πr^2\cdot H \\
V=\frac{1}{3}π\cdot4^2\cdot6 \\
V=\frac{1}{3}π\cdot16\cdot6 \\
V=\frac{1}{3}π\cdot96 \\
V=32π$$
Odpowiedź:
C. \(32π\)

