Rozwiąż nierówność: \(x^2-14x+24\gt0\).
Współczynniki: \(a=1,\;b=-14,\;c=24\)
$$Δ=b^2-4ac=(-14)^2-4\cdot1\cdot24=196-96=100 \\
\sqrt{Δ}=\sqrt{100}=10$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-14)-10}{2\cdot1}=\frac{14-10}{2}=\frac{4}{2}=2 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-14)+10}{2\cdot1}=\frac{14+10}{2}=\frac{24}{2}=12$$
Ustalmy sobie na początek kształt tej paraboli. Z racji tego iż współczynnik \(a\) jest dodatni, to na pewno ramiona tej paraboli będą skierowane do góry. Zaznaczamy więc na osi miejsca zerowe obliczone przed chwilą i szkicujemy parabolę:
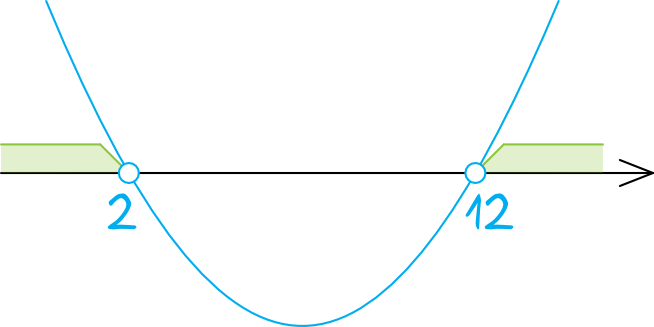
Kropki są niezamalowane, bo w nierówności wystąpił znak \(\gt\).
Patrzymy w których miejscach funkcja przyjmuje wartości większe od zera, czyli dla jakich przedziałów wykres znalazł się nad osią.
$$x\in(-\infty;2)\cup(12;+\infty)$$
\(x\in(-\infty;2)\cup(12;+\infty)\).

