Średnice \(AB\) i \(CD\) okręgu o środku \(S\) przecinają się pod kątem \(50°\) (tak jak na rysunku).
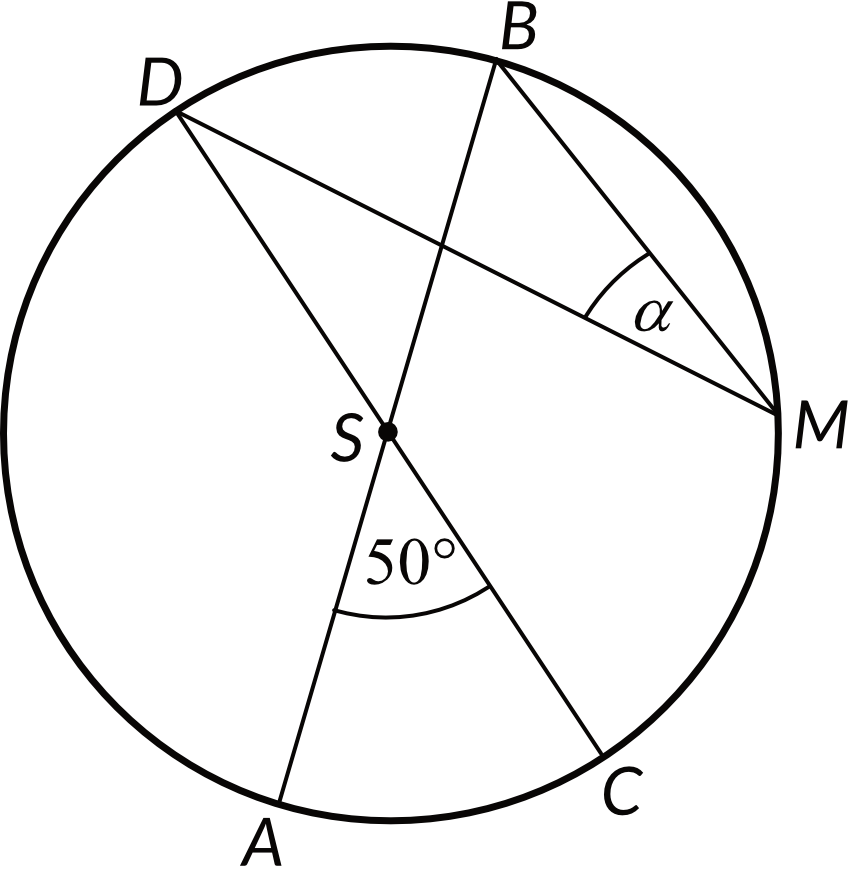
Miara kąta \(α\) jest równa:
\(25°\)
\(30°\)
\(40°\)
\(50°\)
Rozwiązanie:
W tym zadaniu musimy zauważyć, że kąt wpisany \(DMB\) jest oparty na tym samym łuku co kąt środkowy \(DSB\). Gdybyśmy więc znali miarę kąta \(DSB\) to moglibyśmy stwierdzić, że kąt \(α\) jest od niego dwa razy mniejszy.
Kąt \(DSB\) jest kątem wierzchołkowym względem kąta \(ASC\) który ma \(50°\), a to oznacza, że \(|\sphericalangle DSB|=50°\). Po tym ustaleniu już wiemy, że kąt \(α\) będzie miał dwa razy miejszą miarę, czyli \(α=25°\).
Odpowiedź:
A. \(25°\)


Skąd wiadomo, że alfa będzie miał dwa razy mniejszą miarę?
Wynika to z własności kątów środkowych i wpisanych, które oparte są na tym samym łuku. Zgodnie z zasadą – jeżeli dwa kąty są oparte na tym samym łuku (a tak jest właśnie w tym zadaniu), to miara kąta wpisanego jest dwa razy mniejsza od miary kąta środkowego :)