Wykres funkcji kwadratowej

Wykresem funkcji kwadratowej jest parabola, która może mieć ramiona skierowane do góry albo do dołu. Przykładowo:

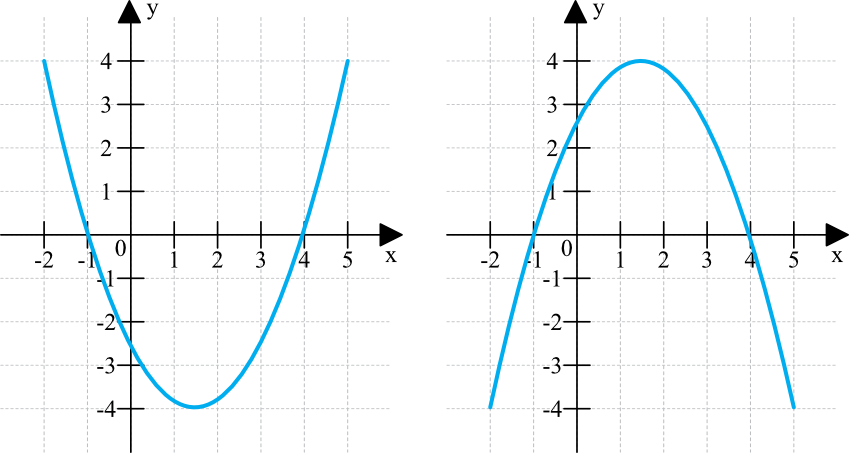
Temat poświęcony wykresowi funkcji kwadratowej zaczniemy od umiejętności rysowania paraboli. Kiedy chcieliśmy narysować wykres funkcji liniowej wystarczyło wyznaczyć wartości dwóch punktów przechodzących przez prostą. Tutaj niestety dwa punkty nie wystarczą, bo istnieje cała masa różnych możliwości ułożenia paraboli przechodzącej przez dwa punkty. Jak więc narysować wykres funkcji kwadratowej?

1. Musimy obliczyć miejsca zerowe funkcji, przyrównując wartość funkcji do zera i rozwiązując odpowiednie równanie kwadratowe.
2. Musimy ustalić, czy ramiona paraboli są skierowane do góry, czy do dołu. O ułożeniu ramion decyduje współczynnik kierunkowy $a$. Jeżeli $a\gt0$ to ramiona są skierowane do góry. Jeżeli $a\lt0$ to ramiona są skierowane do dołu.

Te dwa powyższe punkty są obowiązkowe, aby móc narysować w miarę dokładnie wykres funkcji kwadratowej. Chcąc narysować parabolę jeszcze precyzyjniej możemy wykonać następujące kroki:
3. Możemy obliczyć współrzędne wierzchołka paraboli $W=(p;q)$ korzystając ze wzorów $p=\frac{-b}{2a}$ oraz $q=\frac{-Δ}{4a}$.
4. Możemy obliczyć punkt przecięcia się wykresu z osią igreków. W tym celu do wzoru funkcji wystarczy podstawić argument $x=0$ lub pamiętać, że o miejscu przecięcia decyduje współczynnik $c$.

Brzmi to dość skomplikowanie, dlatego rozpatrzmy to sobie wszystko na konkretnym przykładzie:

Przykład 1. Narysuj wykres funkcji kwadratowej $y=x^2-6x+5$.

Zaczniemy od wyznaczenia miejsc zerowych. Szukamy miejsc zerowych, czyli musimy przyrównać wzór funkcji do zera. Powstanie nam zatem równanie kwadratowe $x^2-6x+5=0$. To równanie jest przedstawione w postaci ogólnej, zatem miejsca zerowe wyliczymy korzystając z klasycznej delty:
Współczynniki: $a=1,\;b=-6,\;c=5$
$$Δ=b^2-4ac=(-6)^2-4\cdot1\cdot5=36-20=16 \\
\sqrt{Δ}=\sqrt{16}=4$$

$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-6)-4}{2\cdot1}=\frac{6-4}{2}=\frac{2}{2}=1 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-6)+4}{2\cdot1}=\frac{6+4}{2}=\frac{10}{2}=5$$

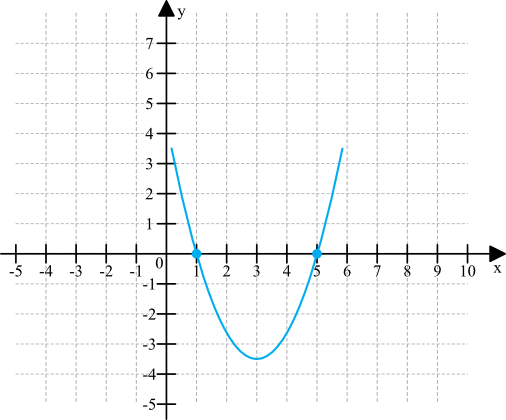
Obliczyliśmy, że miejscami zerowymi funkcji są $x=1$ oraz $x=5$. Widzimy też, że współczynnik kierunkowy $a=1$, czyli jest dodatni. To oznacza, że ramiona paraboli będą skierowane do góry. Te dwie informacje wystarczą nam do narysowania całkiem niezłego rysunku wykresu funkcji kwadratowej:
wykres funkcji kwadratowej

Jeżeli chcemy narysować wykres nieco dokładniej to powinniśmy np. ustalić współrzędne wierzchołka paraboli $W=(p;q)$. W tym celu skorzystamy ze wzorów $p=\frac{-b}{2a}$ oraz $q=\frac{-Δ}{4a}$. Całość obliczeń nie będzie już trudna, bo wszystkie współczynniki mamy wypisane i deltę mamy także policzoną. Musimy jedynie podstawić odpowiednie liczby:
$$p=\frac{-b}{2a} \\
p=\frac{-(-6)}{2\cdot1} \\
p=\frac{6}{2} \\
p=3$$

$$q=\frac{-Δ}{4a} \\
q=\frac{-16}{4\cdot1} \\
q=-4$$

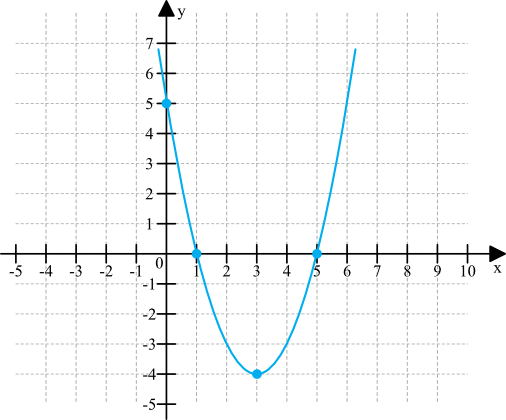
Wyszło nam, że wierzchołek paraboli znajduje się w punkcie $W=(3;-4)$.

Na sam koniec możemy jeszcze ustalić jakie jest miejsce przecięcia się paraboli z osią igreków, czyli po prostu jaką wartość przyjmuje funkcja dla argumentu $x=0$. Podstawiając $x=0$ do wzoru otrzymamy:
$$y=x^2-6x+5 \\
y=0^2-6\cdot0+5 \\
y=0-0+5 \\
y=5$$

Równie dobrze informację o miejscu przecięcia się z osią igreków możemy odczytać ze współczynnika $c$. Skoro $c=5$, to oś igreków jest przecinana dla $y=5$.

W ten sposób ustaliliśmy, że parabola przecina oś igreków dla $y=5$, czyli po prostu w punkcie $A=(0;5)$. Wykorzystując dodatkowe informacje na temat współrzędnych wierzchołka oraz miejsca przecięcia się z osią igreków możemy narysować nasz wykres nieco precyzyjniej:
wykres funkcji kwadratowej

Rysowanie wykresów mamy dość szczegółowo omówione. Teraz spójrzmy jakie kluczowe informacje możemy odczytać z wykresu takiej funkcji:

Przykład 2. Omów podstawowe własności poniższej funkcji:

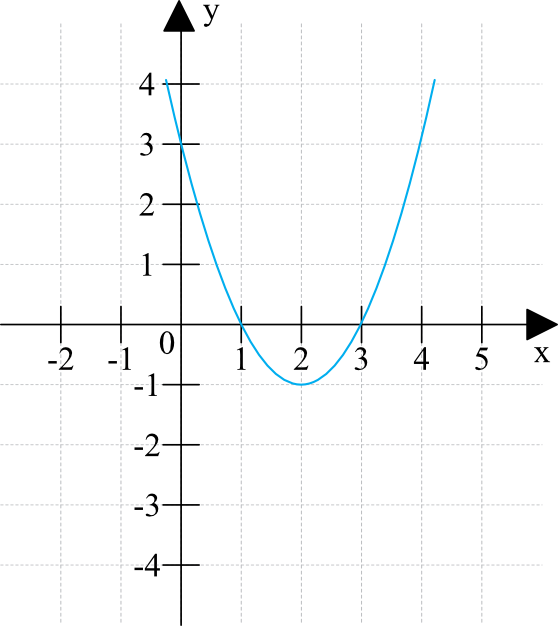
Dziedzina: $x\in\mathbb{R}$
Zbiór wartości: $y\in\langle-1;+\infty)$
Miejsca zerowe: $x_{1}=1$ oraz $x_{2}=3$
Punkt przecięcia z osią igreków: $y=3$
Funkcja rośnie w przedziale: $x\in\langle2;+\infty)$
Funkcja maleje w przedziale: $x\in(-\infty;2\rangle$
Funkcja przyjmuje wartości dodatnie dla $x\in(-\infty;1)$ oraz $x\in(3;\infty)$
Funkcja przyjmuje wartości ujemne dla $x\in(1;3)$

Możemy jeszcze na podstawie tego wykresu określić, że:
Współczynnik $a\gt0$ (bo funkcja jest rosnąca)
Współczynnik $c=3$ (bo funkcja przecina oś igreków dla $y=3$)

Spójrzmy także na inne przykładowe zadania związane z wykresami funkcji:

Przykład 3. Na którym rysunku przedstawiono wykres funkcji $y=x^2+3x-4$?

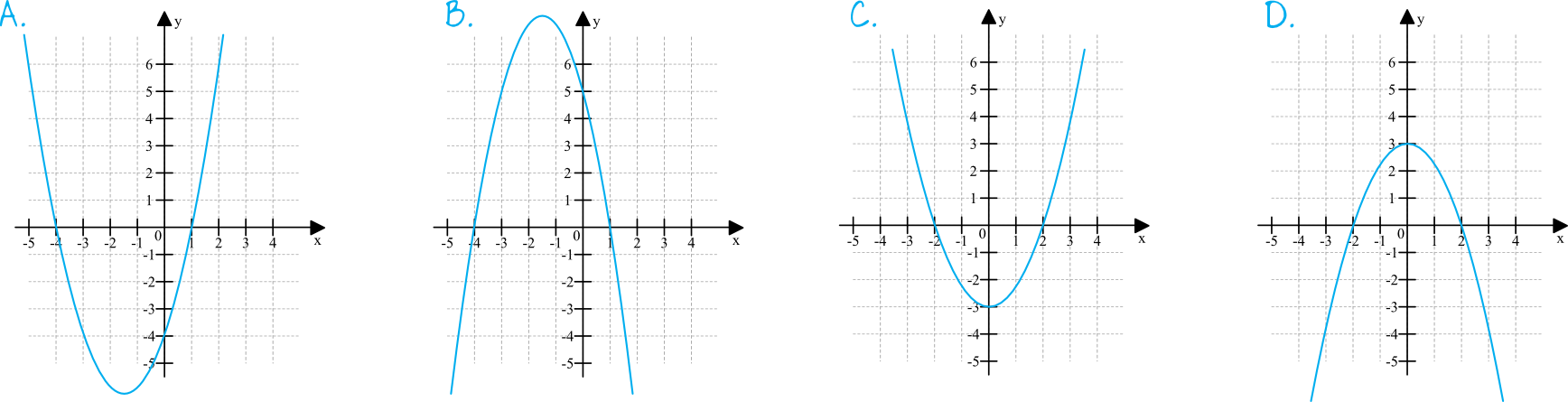
Na samym początku najprościej jest określić kierunek ułożenia ramion. Nasza funkcja kwadratowa ma współczynnik kierunkowy $a=1$, zatem interesują nas rysunki na których parabola ma ramiona skierowane do góry. Już na podstawie tej prostej analizy możemy odrzucić dwie odpowiedzi. Zostają nam zatem dwie możliwości A oraz C.

Bardzo szybko możemy też określić miejsce przecięcia się paraboli z osią igreków, o ile pamiętamy że decyduje o tym współczynnik $c$. Nasza funkcja ma współczynnik $c=-4$, zatem funkcja powinna przeciąć oś igreków dla $y=-4$. Taka sytuacja ma miejsce jedynie na rysunku A, więc to musi być nasza prawidłowa odpowiedź.

Ale to nie są jedyne sposoby na rozwiązanie takich zadań. Możemy przykładowo wybrać sobie kilka argumentów np. $x=0, x=1, x=2$ i sprawdzić jakie wartości osiągnie nasza funkcja. W ten sposób poznamy kilka punktów przez które przechodzi nasza parabola:
Gdy $x=0$ to mamy $0^2+3\cdot0-4=0+0-4=-4$
Gdy $x=1$ to mamy $1^2+3\cdot1-4=1+3-4=4-4=0$
Gdy $x=2$ to mamy $2^2+3\cdot2-4=4+6-4=10-4=6$

Teraz musimy już tylko sprawdzić na którym wykresie funkcja przyjmuje poszczególne wartości dla danych argumentów.

Dobrą (choć nieco czasochłonną metodą) jest też wyznaczenie miejsc zerowych takiej funkcji, co także umożliwi nam weryfikację niektórych odpowiedzi.

Przykład 4. Wyznacz współrzędne wierzchołka paraboli będącej wykresem funkcji $y=2x^2+5x+3$.

Wierzchołek paraboli $W=(p;q)$ obliczymy korzystając ze wzorów $p=\frac{-b}{2a}$ oraz $q=\frac{-Δ}{4a}$.
$$p=\frac{-b}{2a} \\
p=\frac{-5}{2\cdot2} \\
p=\frac{-5}{4} \\
p=-1\frac{1}{4}$$

Do współrzędnej $q$ potrzebujemy znać wartość delty, zatem:
Współczynniki: $a=2,\;b=5,\;c=3$
$$Δ=b^2-4ac=5^2-4\cdot2\cdot3=25-24=1$$

$$q=\frac{-Δ}{4a} \\
q=\frac{-1}{4\cdot2} \\
q=-\frac{1}{8}$$

To oznacza, że wierzchołek paraboli ma współrzędne $W=\left(-1\frac{1}{4};-\frac{1}{8}\right)$.

Przykład 5. W jakim przedziale funkcja kwadratowa $y=-2x^2+8x-5$ jest rosnąca?

Funkcja kwadratowa zawsze rośnie lub maleje od minus nieskończoności do wierzchołka lub od wierzchołka do plus nieskończoności (to warto zapamiętać). Nasza funkcja będzie mieć ramiona skierowane do dołu, bo współczynnik kierunkowy $a$ jest ujemny ($a=-2$), zatem całość będzie wyglądać mniej więcej w ten sposób:
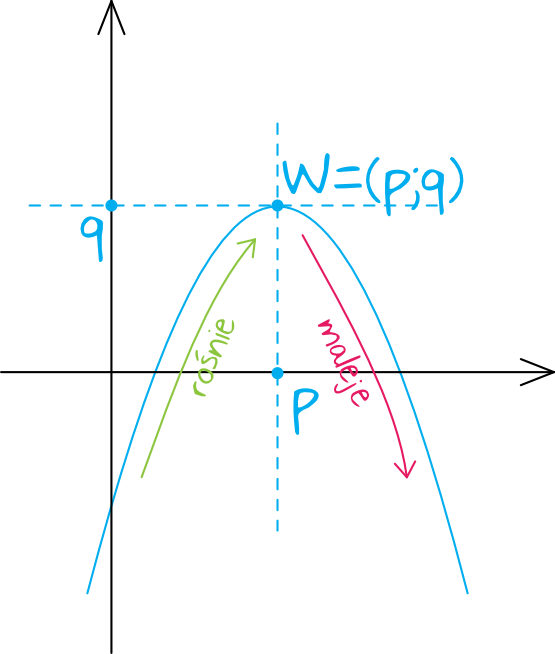
wykres funkcji kwadratowej

Musimy więc poznać współrzędne wierzchołka, a w zasadzie to wystarczy nam współrzędna $p$. Z rysunku wynika jasno, że funkcja rośnie w przedziale $(-\infty;p)$. Wartość $q$ jest dla nas w tym momencie nieistotna. W związku z tym:
$$p=\frac{-b}{2a} \\
p=\frac{-8}{2\cdot(-2)} \\
p=\frac{-8}{-4} \\
p=2$$

To oznacza, że funkcja jest rosnąca w przedziale $(-\infty;2\rangle$.

Zobacz też: Postać ogólna, iloczynowa i kanoniczna funkcji kwadratowej

Zobacz też: Miejsca zerowe funkcji kwadratowej