Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Sytuacja z treści zadania będzie wyglądać mniej więcej w ten oto sposób:
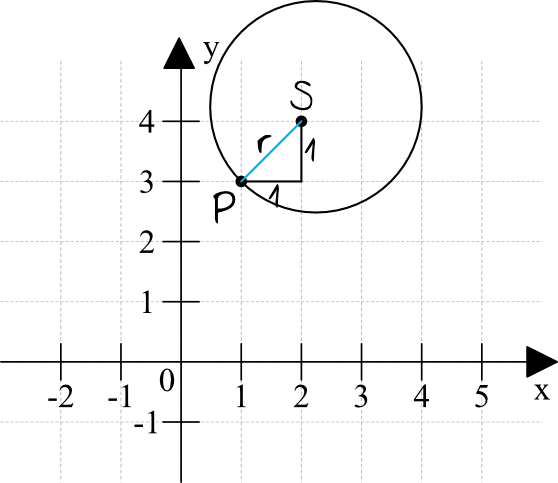
Krok 2. Obliczenie długości promienia okręgu.
Długość promienia okręgu możemy obliczyć korzystając ze wzoru na długość odcinka. Jednak prościej będzie skorzystać z rysunku pomocniczego, bowiem wprost widzimy, że utworzył nam się tutaj trójkąt prostokątny o przyprostokątnych o długości \(1\) (taka połówka kwadratu). Możemy więc od razu zauważyć, że \(r=\sqrt{2}\) (bo przekątna kwadratu jest \(\sqrt{2}\) razy dłuższa od boku kwadratu). Ewentualnie możemy posłużyć się Twierdzeniem Pitagorasa:
$$1^2+1^2=r^2 \\
1+1=r^2 \\
r^2=2 \\
r=\sqrt{2} \quad\lor\quad r=-\sqrt{2}$$
Ujemny wynik oczywiście odrzucamy, zatem zostaje nam \(r=\sqrt{2}\).
Krok 3. Obliczenie długości okręgu.
Korzystając ze wzoru na obwód okręgu możemy zapisać, że:
$$Obw=2\pi r \\
Obw=2\pi\cdot\sqrt{2}$$