Rozwiązanie
Krok 1. Zapisanie nierówności w postaci ogólnej.
Aby przystąpić do wykonywania obliczeń musimy przenieść wszystkie wyrazy na lewą stronę, tak aby po prawej stronie zostało nam tylko zero. Zatem:
$$\left(x-\frac{1}{2}\right)x\gt3\left(x-\frac{1}{2}\right)\left(x+\frac{1}{3}\right) \\
\left(x-\frac{1}{2}\right)x-3\left(x-\frac{1}{2}\right)\left(x+\frac{1}{3}\right)\gt0$$
Wbrew pozorom nie jest to postać iloczynowa z której łatwo moglibyśmy wyznaczyć miejsca zerowe, bo w środku całego wyrażenia pojawia nam się odejmowanie. W związku z tym musimy uprościć całe wyrażenie w następujący sposób:
$$x^2-\frac{1}{2}x-\left(3x-\frac{3}{2}\right)\left(x+\frac{1}{3}\right)\gt0 \\
x^2-\frac{1}{2}x-\left(3x^2+x-\frac{3}{2}x-\frac{3}{6}\right)\gt0 \\
x^2-\frac{1}{2}x-3x^2-x+\frac{3}{2}x+\frac{1}{2}\gt0 \\
-2x^2+\frac{1}{2}\gt0$$
Krok 2. Obliczenie miejsc zerowych wielomianu.
Powstała nam nierówność kwadratowa, zatem musimy najpierw obliczyć miejsca zerowe, a zrobimy to tradycyjnie przy pomocy delty:
Współczynniki: \(a=-2,\;b=0,\;c=\frac{1}{2}\)
$$Δ=b^2-4ac=0^2-4\cdot(-2)\cdot\frac{1}{2}=0-(-4)=0+4=4 \\
\sqrt{Δ}=\sqrt{4}=2$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-0-2}{2\cdot(-2)}=\frac{-2}{-4}=\frac{1}{2} \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-0+2}{2\cdot(-2)}=\frac{2}{-4}=-\frac{1}{2}$$
Krok 3. Szkicowanie wykresu paraboli.
Współczynnik \(a\) był ujemny, więc parabola będzie mieć ramiona skierowane do dołu. Zaznaczamy na osi wyliczone przed chwilą miejsca zerowe (z pustymi kropkami, bo w nierówności wystąpił znak \(\gt\)).
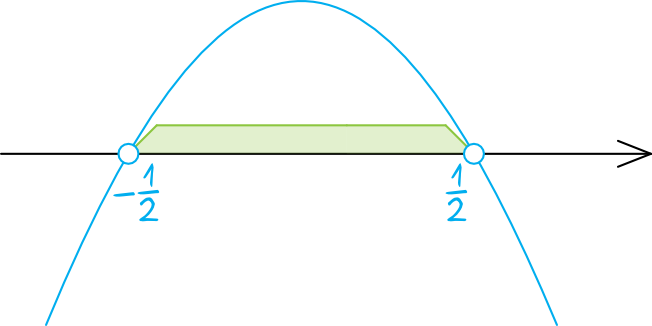
Szukamy argumentów dla których funkcja przyjmuje wartości większe od zera, a więc interesować nas będzie przedział:
$$x\in\left(-\frac{1}{2};\frac{1}{2}\right)$$