Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Narysujmy sobie układ współrzędnych, zaznaczmy znane nam punkty oraz poszukiwany kąt ostry:
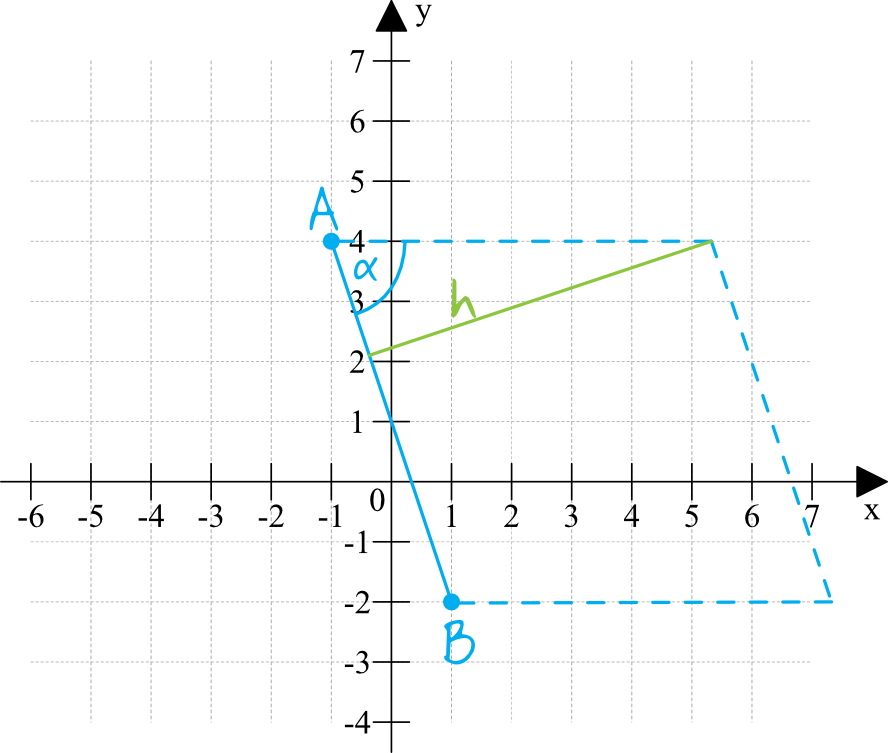
Z rysunku jasno wynika, że do obliczenia sinusa kąta α będziemy potrzebować znać wysokość rombu oraz długość jego boku.
Krok 2. Obliczenie długości boku rombu.
Znając współrzędne obydwu punktów możemy obliczyć długość odcinka \(AB\) (czyli długość boku rombu):
$$|AB|=\sqrt{(1-(-1))^2+(-2-4)^2} \\
|AB|=\sqrt{2^2+(-6)^2} \\
|AB|=\sqrt{4+36} \\
|AB|=\sqrt{40} \\
|AB|=\sqrt{4\cdot10} \\
|AB|=2\sqrt{10}$$
Możemy więc powiedzieć, że romb ma bok o długości \(a=2\sqrt{10}\).
Krok 3. Obliczenie wysokości rombu.
Pole rombu możemy obliczyć ze wzoru \(P=ah\). Skoro \(P=30\) oraz \(a=2\sqrt{10}\), to:
$$30=2\sqrt{10}\cdot h \\
h=\frac{30}{2\sqrt{10}} \\
h=\frac{15}{\sqrt{10}} \\
h=\frac{15\cdot\sqrt{10}}{\sqrt{10}\cdot\sqrt{10}} \\
h=\frac{15\sqrt{10}}{10} \\
h=\frac{3\sqrt{10}}{2}$$
Krok 4. Obliczenie wartości sinusa kąta \(α\).
Znając długość boku rombu oraz jego wysokość możemy teraz zapisać, że:
$$sinα=\frac{h}{a} \\
sinα=\frac{\frac{3\sqrt{10}}{2}}{2\sqrt{10}} \\
sinα=\frac{3\sqrt{10}}{2}:2\sqrt{10} \\
sinα=\frac{3\sqrt{10}}{2}\cdot\frac{1}{2\sqrt{10}} \\
sinα=\frac{3}{4}$$