Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Kluczowym problemem w tym zadaniu jest obliczenie długości "ukośnych" odcinków. Pomoże nam w tym jednak Twierdzenie Pitagorasa:
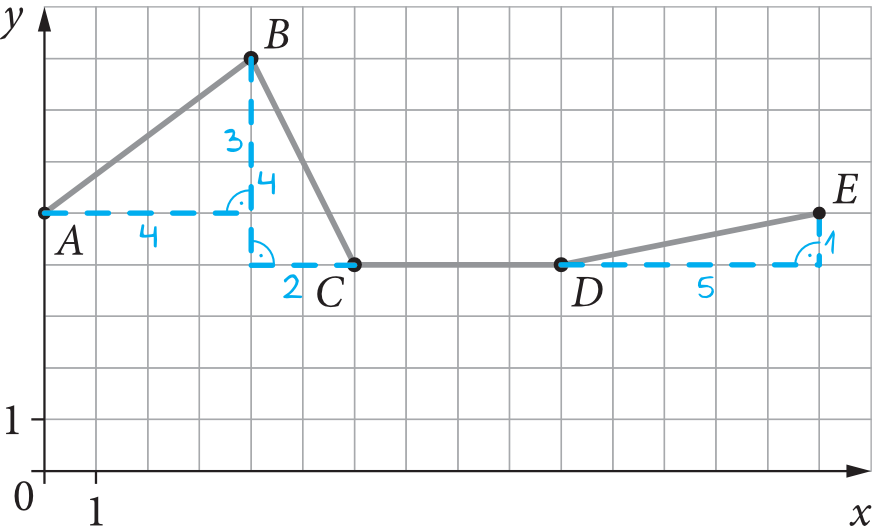
Krok 2. Obliczenie długości poszczególnych odcinków.
Zacznijmy od odcinka \(AB\). Tutaj powinniśmy dostrzec, że jest to po prostu klasyczny trójkąt prostokątny o bokach \(3, 4, 5\), zatem odcinek \(|AB|=5\). Jeśli tego nie dostrzegamy, to możemy oczywiście skorzystać z Twierdzenia Pitagorasa.
Teraz przejdźmy do odcinka \(BC\). Tym razem nie obejdzie się bez Twierdzenia Pitagorasa, zatem:
$$2^2+4^2=|BC|^2 \\
4+16=|BC|^2 \\
|BC|^2=20 \\
|BC|=\sqrt{20} \quad\lor\quad |BC|=-\sqrt{20}$$
Ujemny wynik oczywiście odrzucamy, zatem zostaje nam \(|BC|=\sqrt{20}\) i w takiej postaci możemy to zostawić.
Odcinek \(CD\) jest najprostszy, bowiem wystarczy policzyć jego długość po kratkach. Tutaj możemy wprost zapisać, że \(|CD|=4\).
Na koniec został odcinek \(DE\) i tak jak w przypadku odcinka \(BC\), musimy skorzystać z Twierdzenia Pitagorasa:
$$5^2+1^2=|DE|^2 \\
25+1=|DE|^2 \\
|DE|^2=26 \\
|DE|=\sqrt{26} \quad\lor\quad |DE|=-\sqrt{26}$$
Interesuje nas tylko dodatni wynik, zatem \(|DE|=\sqrt{26}\).
Krok 3. Ustalenie, który chłopiec miał racje.
Długości boków są następujące:
\(|AB|=5\)
\(|BC|=\sqrt{20}\) (czyli więcej niż \(4\), ale mniej niż \(5\))
\(|CD|=4\)
\(|DE|=\sqrt{26}\) (czyli więcej niż \(5\))
To oznacza, że:
$$|CD|\lt|BC|\lt|AB|\lt|DE|$$
Rację miał więc Bernard.