Do tej pory wszystko czego uczyliśmy się z geometrii było związane z figurami płaskimi. Czas więc przejść do tematu, w którym poznamy takie słowa jak objętość, czy też bryła. Przed Tobą pierwsze figury przestrzenne – prostopadłościan i sześcian
Z prostopadłościanami masz styczność na co dzień. Przedmiotami z życia codziennego, które są prostopadłościanami będą np. sok w kartonie, Twój podręcznik do matematyki czy też pudełko zapałek. Co więc wyróżnia prostopadłościany od innych brył?
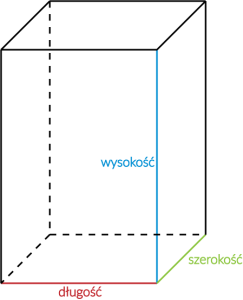
- prostopadłościany mają trzy wymiary: wysokość, długość i szerokość
- mają \(6\) ścian i wszystkie z nich są prostokątami (z których część jest względem siebie równoległa, a część prostopadła)
- mają \(12\) krawędzi
- mają \(8\) wierzchołków
Tak wygląda przykładowy prostopadłościan:
W każdym prostopadłościanie wyróżniamy trzy wymiary – wysokość, długość i szerokość.
Sześcian jest bryłą bardzo zbliżoną do prostopadłościanu, z tą różnicą że wszystkie ściany tej bryły są kwadratami. To jednocześnie oznacza, że wszystkie krawędzie sześcianu mają jednakową długość (warto o tym pamiętać, bo ta wiedza przyda nam się na najbliższych zajęciach).
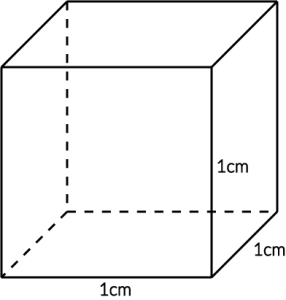
W sześcianie wszystkie wymiary (długość, szerokość, wysokość) mają jednakową miarę. W tym przypadku jest to 1cm.
Krok 1. Żeby obliczyć takie zadanie musimy znać trzy miary – wysokość, długość oraz szerokość prostopadłościanu. Wszystkie te miary zostały podane w zadaniu, więc możemy przejść do kolejnego kroku.
Krok 2. Jeśli przyjrzysz się uważnie prostopadłościanowi to zauważysz, że każda miara krawędzi pojawia się w bryle czterokrotnie.
Krok 3. Jeśli więc prostopadłościan ma wymiary \(3cm\;x\;5cm\;x\;2cm\), to suma długości jego krawędzi jest równa:
$$3cm\cdot4+5cm\cdot4+2cm\cdot4=12cm+20cm+8cm=40cm \\
\text{lub} \\
(3cm+5cm+2cm)\cdot4=10cm\cdot4=40cm$$
W przypadku sześcianu pamiętaj, że wszystkie krawędzie (a jest ich łącznie \(12\)) mają tą samą długość.
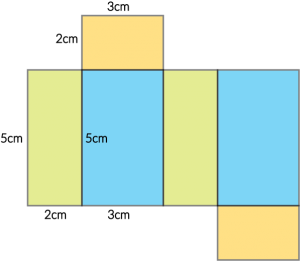
Krok 1. Spójrzmy jak będzie wyglądać przykładowa siatka naszego prostopadłościanu.
Krok 2. Kolory ścian pokazują nam, które ściany mają tą samą powierzchnię. Wystarczy więc obliczyć pola trzech różnokolorowych prostokątów, a później wynik pomnożyć przez \(2\). W naszym przypadku będzie to:
I ściana (zielona): \(5cm\cdot2cm=10cm^2\)
II ściana (niebieska): \(3cm\cdot5cm=15cm^2\)
III ściana (pomarańczowa): \(3cm\cdot2cm=6cm^2\)
Pole powierzchni tego prostopadłościanu jest więc równe:
$$(10cm^2+15cm^2+6cm^2)\cdot2=31cm^2\cdot2=62cm^2$$
(mnożymy przez \(2\), bo każda ściana występuje dwukrotnie)
Zadania kontrolne:
- Odpowiedź: Takimi przedmiotami/obiektami mogą być np. akwarium, pralka, lodówka, wagon kolejowy, różne kartony i pudełka, szafa, blok mieszkalny.
Zobacz także inne tematy i ćwiczenia związane z prostopadłościanami i sześcianami:
wiem wszystko a mam tylko 8lat
ty to chyba już do liceum chodzisz xd
NIE WIEM NIC A MAM 15 LAT
szukam czegoś na kartkówkę z prostopadłości i sześcianu
Ja też
Fajny sprawdzian z tego działu jest tutaj:
https://szaloneliczby.pl/prostopadlosciany-i-szesciany-sprawdzian-klasa-5/
super stronka dla uczniów
Ta strona jest bardzo pomocna ;)
bardzo mi sie to podoba
bardzo fajne,polecam xd
Fajna strona