Przekątna przekroju osiowego walca, którego promień podstawy jest równy \(4\) i wysokość jest równa \(6\), ma długość:
\(\sqrt{10}\)
\(\sqrt{20}\)
\(\sqrt{52}\)
\(10\)
Rozwiązanie:
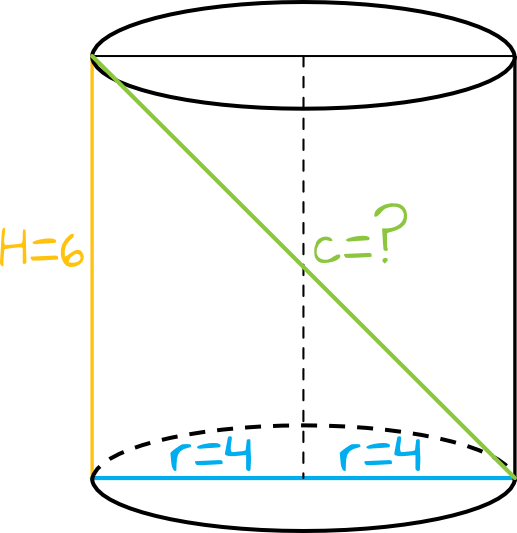
Skoro promień podstawy walca jest równy \(4\), to prostokąt znajdujący się w przekroju będzie miał podstawę równą \(4\cdot2=8\) (patrz rysunek). Do tego znamy wysokość walca, tak więc przekątną przekroju możemy obliczyć z Twierdzenia Pitagorasa.
$$a^2+b^2=c^2 \\
8^2+6^2=c^2 \\
64+36=c^2 \\
c^2=100 \\
c=10$$
Odpowiedź:
D. \(10\)

