Z sześcianu \(ABCDEFGH\) o krawędzi długości a odcięto ostrosłup \(ABDE\) (zobacz rysunek).
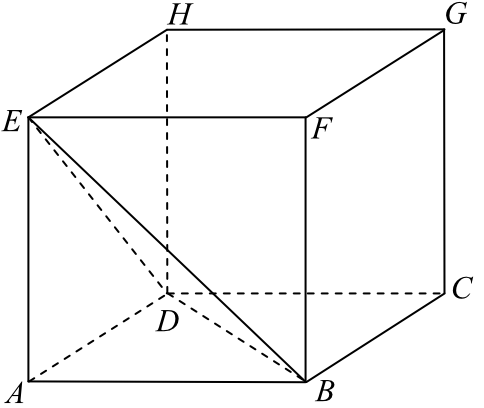
Ile razy objętość tego ostrosłupa jest mniejsza od objętości pozostałej części sześcianu?
\(2\) razy
\(3\) razy
\(4\) razy
\(5\) razy
Rozwiązanie:
Krok 1. Obliczenie pola podstawy ostrosłupa.
Musimy obliczyć pole powierzchni trójkąta \(ABD\), który jest podstawą tego ostrosłupa. Jest to połowa kwadratu o boku \(a\), zatem:
$$P_{p}=\frac{1}{2}a^2$$
Krok 2. Obliczenie objętości ostrosłupa.
Pole podstawy ostrosłupa obliczyliśmy przed chwilą. Wysokość ostrosłupa \(H=a\), bo jest to sześcian, zatem:
$$V_{o}=\frac{1}{3}P_{p}\cdot H \\
V_{o}=\frac{1}{3}\cdot\frac{1}{2}a^2\cdot a \\
V_{o}=\frac{1}{6}a^3$$
Krok 3. Obliczenie objętości pozostałej części sześcianu.
Cały sześcian ma objętość równą \(V=a^3\). Aby więc obliczyć objętość pozostałej części (bo to do niej musimy się odnieść) to musimy od objętości sześcianu odjąć obliczoną przed chwilą objętość ostrosłupa:
$$V_{p}=a^3-\frac{1}{6}a^3 \\
V_{p}=\frac{5}{6}a^3$$
To oznacza, że objętość ostrosłupa jest pięciokrotnie mniejsza od pozostałej części sześcianu.
Odpowiedź:
D. \(5\) razy

