Promień \(AS\) podstawy walca jest równy wysokości \(OS\) tego walca. Sinus kąta \(OAS\) (zobacz rysunek) jest równy:
Skoro długość promienia podstawy oraz wysokość tego walca są sobie równe, to trójkąt \(SAO\) wygląda mniej więcej w ten sposób:
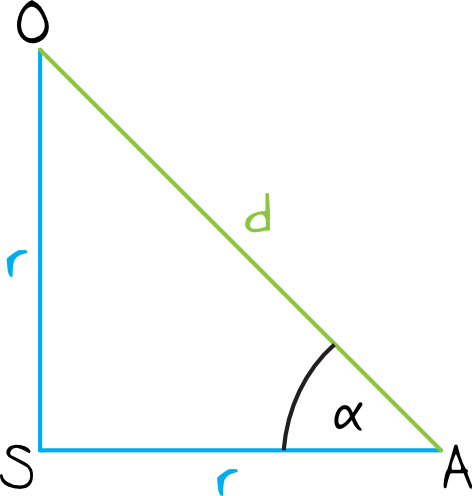
Naszym zadaniem jest wyznaczenie sinusa kąta \(α\). Tak naprawdę można byłoby na tym kroku zakończyć rozwiązywanie tego zadania, bo widzimy że jest to trójkąt równoramienny prostokątny, a więc kąt ostry musi mieć miarę \(α=45°\). Skoro tak, to możemy odczytać z tablic, że:
$$sin45°=\frac{\sqrt{2}}{2}$$
Gdybyśmy jednak nie dostrzegli tego, to można dotrzeć do tej wartości trochę dłuższym sposobem.
Już po samym rysunku widzimy, że odcinek \(d\) jest tak jakby przekątną kwadratu o boku długości \(r\), zatem na pewno \(d=r\sqrt{2}\). Gdybyśmy o tym nie pamiętali, to zawsze możemy się jeszcze ratować Twierdzeniem Pitagorasa:
$$r^2+r^2=d^2 \\
2r^2=d^2 \\
d=\sqrt{2r^2} \\
d=r\sqrt{2}$$
Zgodnie z własnościami funkcji trygonometrycznych:
$$\require{cancel}
sinα=\frac{r}{d} \\
sinα=\frac{\cancel{r}}{\cancel{r}\sqrt{2}} \\
sinα=\frac{1}{\sqrt{2}}=\frac{1\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}}=\frac{\sqrt{2}}{2}$$
B. \(\frac{\sqrt{2}}{2}\)

