Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy narysować taki ostrosłup, zaznaczając na nim miary podane w treści zadania:
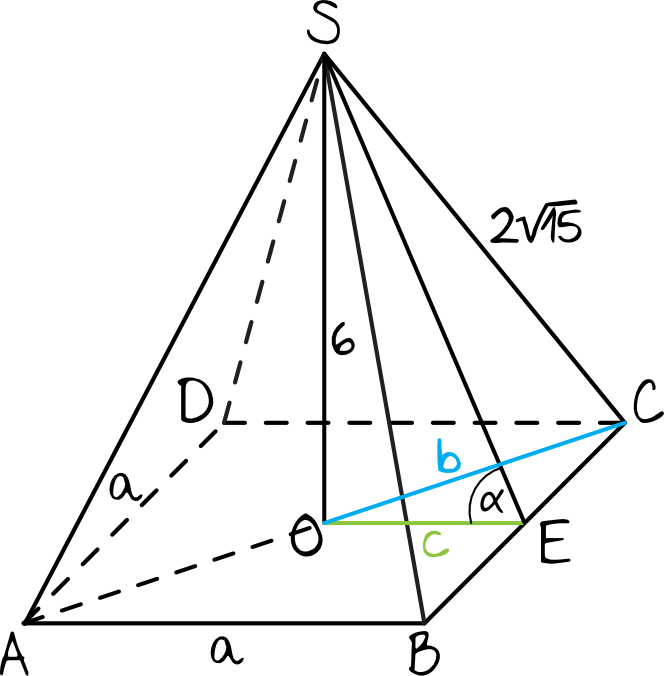
Krok 2. Obliczenie długości przekątnej podstawy.
Spójrzmy na trójkąt prostokątny \(OCS\) , który wytworzył nam się na rysunku. W jego dolnej przyprostokątnej znajduje się odcinek oznaczony jako \(b\), który jest tak naprawdę połową długości przekątnej podstawy (tak nawiasem mówiąc, to w podstawie bryły jest kwadrat, bo jest to ostrosłup prawidłowy czworokątny). Długość tego boku \(b\) możemy obliczyć z Twierdzenia Pitagorasa:
$$b^2+6^2=(2\sqrt{15})^2 \\
b^2+36=4\cdot15 \\
b^2+36=60 \\
b=\sqrt{24} \quad\lor\quad b=-\sqrt{24}$$
Ujemną długość odrzucamy, zatem wiemy już że \(b=\sqrt{24}=\sqrt{4\cdot6}=2\sqrt{6}\).
To też oznacza, że cała przekątna \(AC\) ma miarę \(d=2\cdot2\sqrt{6}=4\sqrt{6}\).
Krok 3. Obliczenie długości krawędzi podstawy.
Już wiemy, że w podstawie naszej bryły musi znajdować się kwadrat. Jedną z własności kwadratu jest to, że kwadrat o boku \(a\) ma przekątną o długości \(a\sqrt{2}\). Ta własność pozwoli nam uzyskać informację na temat długości krawędzi bocznej, bo skoro przekątna ma długość \(4\sqrt{6}\), to:
$$a\sqrt{2}=4\sqrt{6} \\
a=4\sqrt{6}:\sqrt{2} \\
a=4\sqrt{3}$$
Krok 4. Obliczenie długości boku \(c\).
Bok oznaczony jako \(c\) jest połową podstawy, którą przed chwilą wyliczyliśmy, zatem:
$$c=\frac{1}{2}\cdot4\sqrt{3} \\
c=2\sqrt{3}$$
Krok 5. Wyznaczenie miary kąta \(α\).
Spójrzmy teraz na trójkąt prostokątny \(OES\). Znajomość długości boku \(c\) oraz znajomość wysokości ostrosłupa otwierają nam drogę do poznania poszukiwanej miary kąta. Korzystając z tangensa możemy zapisać, że:
$$tgα=\frac{6}{2\sqrt{3}} \\
tgα=\frac{6\cdot\sqrt{3}}{2\sqrt{3}\cdot\sqrt{3}} \\
tgα=\frac{6\cdot\sqrt{3}}{2\cdot3} \\
tgα=\frac{6\cdot\sqrt{3}}{6} \\
tgα=\sqrt{3}$$
Teraz musimy odczytać z tablic dla jakiej miary kąta tangens przyjmuje wartość równą \(\sqrt{3}\) i widzimy, że jest to kąt \(60°\).