W ostrosłupie czworokątnym, w którym wszystkie krawędzie mają tę samą długość, kąt nachylenia krawędzi bocznej do płaszczyzny podstawy ma miarę:
Jeżeli ostrosłup czworokątny ma wszystkie krawędzie równej długości to na pewno w podstawie mamy kwadrat. Cały ostrosłup wyglądać będzie mniej więcej w ten sposób:
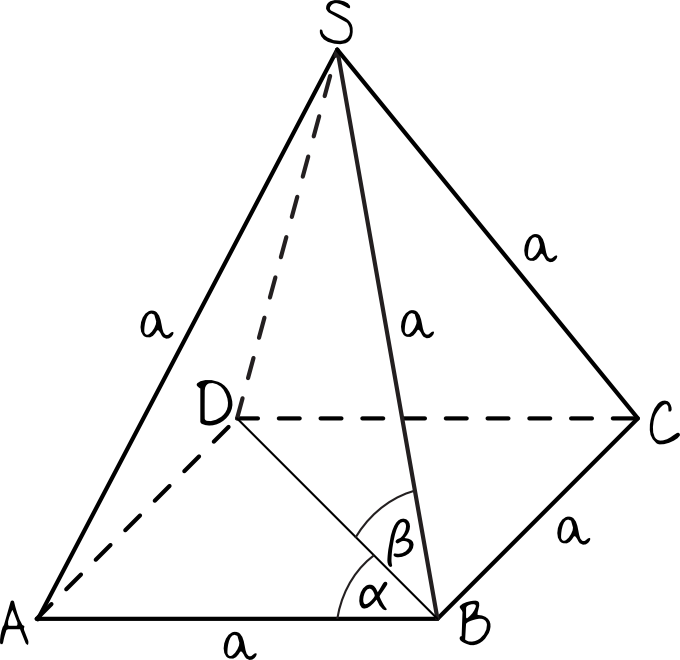
Na rysunku zaznaczyliśmy sobie też dwa kąty – kąt między krawędzią i przekątną podstawy (czyli kąt \(α\)) oraz poszukiwany kąt nachylenia krawędzi bocznej do płaszczyzny podstawy (czyli kąt \(β\)).
Poszukujemy miary kąta \(β\).
Zwróćmy uwagę na to, że trójkąty \(ABD\) oraz \(BDS\) są trójkątami podobnymi (mają te same długości ramion bo krawędzie są sobie równe oraz mają wspólną podstawę trójkąta, która jest przekątną kwadratu). To oznacza, że na naszym rysunku \(α=β\).
Kąt \(α\) ma znaną nam miarę \(45°\), bo przekątna kwadratu dzieli kąt prosty na dwie równe części, czyli \(90°:2=45°\). Skoro tak, to zgodnie z tym co sobie napisaliśmy wcześniej \(β=45°\).
B. \(45°\)

