Pole powierzchni całkowitej walca możemy obliczyć korzystając z następującego wzoru:
$$P_{c}=2πr^2+2πrH$$
gdzie:
\(P_{c}\) – pole powierzchni całkowitej walca
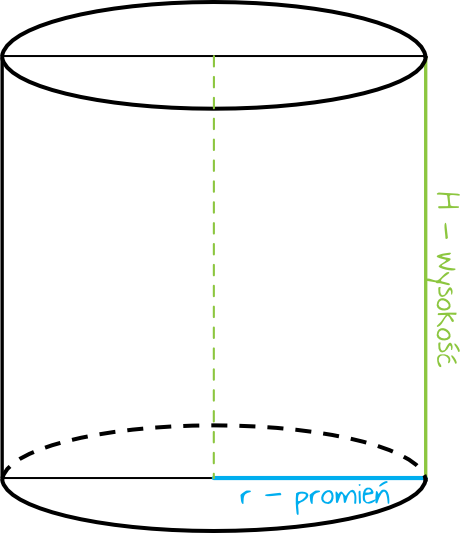
\(r\) – promień podstawy walca
\(H\) – wysokość walca
Bardzo często możemy też się spotkać z lekko przekształconą postacią tego wzoru:
$$P_{c}=2πr(r+H)$$
To co jest jeszcze dość ważne w temacie pola powierzchni to umiejętność oddzielnego obliczenia pola powierzchni bocznej. Wzór na pole powierzchni bocznej jest zaszyty we wzorze na pole powierzchni całkowitej.
Pole powierzchni bocznej obliczymy korzystając ze wzoru:
$$P_{b}=2πrH$$
gdzie:
\(P_{b}\) – pole powierzchni bocznej walca
\(r\) – promień podstawy walca
\(H\) – wysokość walca
Jak teraz dobrze przyjrzymy się tym wzorom to zauważymy, że pole powierzchni całkowitej to tak naprawdę suma pól dwóch podstaw (dolnej i górnej), które są kołami oraz pola powierzchni bocznej. Moglibyśmy więc zapisać, że \(P_{c}=2P_{p}+P_{b}\).
Znamy już wszystkie potrzebne wzory, więc zobaczmy ich wykorzystanie w praktyce.
Podstawiając znane nam dane do wzoru na pole powierzchni całkowitej walca otrzymamy:
$$P_{c}=2πr^2+2πrH \\
P_{c}=2π\cdot4^2+2π\cdot4\cdot7 \\
P_{c}=2π\cdot16+2π\cdot28 \\
P_{c}=32π+56π \\
P_{c}=88π$$
Krok 1. Obliczenie długości promienia podstawy.
Do obliczenia pola powierzchni całkowitej potrzebujemy znać długość promienia podstawy. Korzystając ze wzoru na pole powierzchni bocznej możemy zapisać, że:
$$P_{b}=2πrH \\
60π=2πr\cdot5 \quad\bigg/:π \\
60=10r \\
r=6$$
Krok 2. Obliczenie pola powierzchni całkowitej.
Mamy już komplet danych do obliczenia pola powierzchni całkowitej, bowiem wiemy że \(r=6\) oraz że \(H=5\), zatem:
$$P_{c}=2πr^2+2πrH \\
P_{c}=2π\cdot6^2+2π\cdot6\cdot5 \\
P_{c}=2π\cdot36+60π \\
P_{c}=72π+60π \\
P_{c}=132π$$
Tak na marginesie to zwróć uwagę na to, że w tym ostatnim kroku obliczając nasze pole powierzchni całkowitej, mogliśmy pod \(2πrH\) od razu podstawić wartość \(60π\), bo takie jest przecież nasze pole powierzchni bocznej, które było podane w treści zadania.
