Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Korzystając z informacji z treści zadania oraz z własności stycznych do okręgu możemy sporządzić następujący szkic:
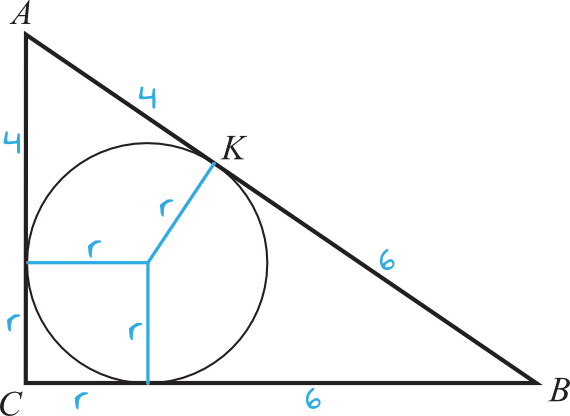
Krok 2. Ułożenie równania.
Skoro jest to trójkąt prostokątny, to możemy zgodnie z Twierdzeniem Pitagorasa zapisać, że:
$$(r+4)^2+(r+6)^2=10^2 \\
r^2+8r+16+r^2+12r+36=100 \\
2r^2+20r+52=100 \\
2r^2+20r-48=0 \quad\bigg/:2 \\
r^2+10r-24=0$$
Dzielenie przez \(2\) nie jest koniecznością, ale dzięki temu potem pracujemy na mniejszych liczbach. Finalnie wynik wyjdzie ten sam.
Krok 3. Rozwiązanie powstałego równania kwadratowego.
Współczynniki: \(a=1,\;b=10,\;c=-24\)
$$Δ=b^2-4ac=10^2-4\cdot1\cdot(-24)=100-(-96)=100+96=196 \\
\sqrt{Δ}=\sqrt{196}=14$$
$$r_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-10-14}{2\cdot1}=\frac{-24}{2}=-12 \\
r_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-10+14}{2\cdot1}=\frac{4}{2}=2$$
Promień nie może być ujemny, zatem jedynym pasującym nam rozwiązaniem jest \(r=2\).