Dane są punkty \(A=(-4,0)\) i \(M=(2,9)\) oraz prosta \(k\) o równaniu \(y=-2x+10\). Wierzchołek \(B\) trójkąta \(ABC\) to punkt przecięcia prostej \(k\) z osią \(Ox\) układu współrzędnych, a wierzchołek \(C\) jest punktem przecięcia prostej \(k\) z prostą \(AM\). Oblicz pole trójkąta \(ABC\).
Zróbmy sobie prosty szkic tej całej sytuacji i zaznaczmy w układzie współrzędnych dane z treści zadania:
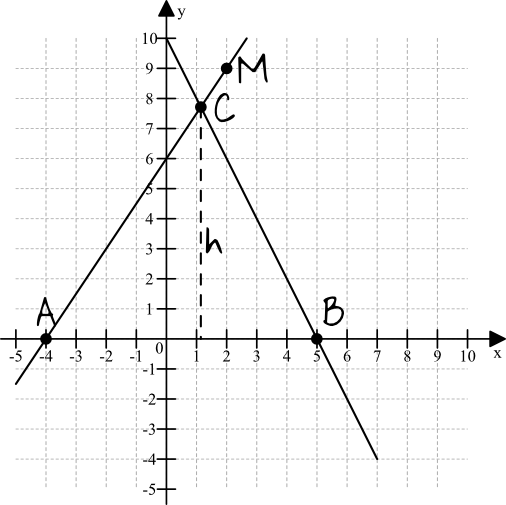
Musimy wyznaczyć współrzędne punktu \(B\) (potrzebne będą do wyznaczenia długości podstawy) oraz współrzędne punktu \(C\) (potrzebne do wyznaczenia wysokości trójkąta).
Wyznaczenie współrzędnych tego punktu jest stosunkowo dość proste, bo jest to tak naprawdę miejsce zerowe prostej \(k\) (tak wynika z treści zadania). Można więc powiedzieć, że \(B=(x;0)\) zatem podstawiając te współrzędne do prostej o równaniu \(y=-2x+10\) otrzymamy:
$$-2x+10=0 \\
-2x=-10 \\
x=5$$
To oznacza, że \(B=(5;0)\).
Skoro znamy współrzędne obydwu tych punktów to możemy skorzystać ze wzoru na równanie prostej albo też zbudować prosty układ równań. Szybciej będzie chyba skorzystać ze wzoru:
$$(y-y_{A})(x_{M}-x_{A})-(y_{M}-y_{A})(x-x_{A})=0 \\
(y-0)(2-(-4))-(9-0)(x-(-4))=0 \\
(y-0)(2+4)-9\cdot(x+4)=0 \\
(y-0)\cdot6-9\cdot(x+4)=0 \\
6y-9x-36=0 \\
6y=9x+36 \quad\bigg/:6 \\
y=\frac{3}{2}x+6$$
Stworzymy układ równań składających się z dwóch prostych, których miejscem przecięcia się są właśnie współrzędne punktu \(C\).
\begin{cases}
y=-2x+10 \\
y=\frac{3}{2}x+6
\end{cases}
Korzystając z metody podstawiania otrzymujemy:
$$-2x+10=\frac{3}{2}x+6 \quad\bigg/\cdot2 \\
-4x+20=3x+12 \\
-7x=-8 \\
x=\frac{8}{7}$$
Współrzędną \(y\) obliczmy podstawiając wartość \(x=\frac{8}{7}\) do jednego z równań:
$$y=-2\cdot\frac{8}{7}+10 \\
y=\frac{-16}{7}+10 \\
y=\frac{-16}{7}+\frac{70}{7} \\
y=\frac{54}{7}$$
Mamy zatem: \(C=\left(\frac{8}{7};\frac{54}{7}\right)\).
Do obliczenia pola trójkąta potrzebujemy jeszcze poznać długości podstawy trójkąta i wysokości.
• Długość podstawy trójkąta: \(|AB|=5+4=9\) (wynika to bezpośrednio z rysunku – pięć jednostek z punktu \(A\) do środka układu współrzędnych plus cztery jednostki ze środka układu współrzędnych do punktu \(B\)).
• Wysokość trójkąta to tak naprawdę współrzędna igrekowa punktu \(C\), czyli \(H=\frac{54}{7}\).
Pole trójkąta jest więc równe:
$$P=\frac{1}{2}\cdot|AB|\cdot H \\
P=\frac{1}{2}\cdot9\cdot\frac{54}{7} \\
P=\frac{1}{2}\cdot\frac{486}{7} \\
P=\frac{243}{7}=34\frac{5}{7}$$
\(P=34\frac{5}{7}\)

