Proste, odcinki, kąty - zadania (egzamin ósmoklasisty)
Zadanie 3. (1pkt) Która z narysowanych niżej liter alfabetu greckiego ma tylko jedną oś symetrii?
Wyjaśnienie:
Jedną oś symetrii ma tylko pierwszy symbol.
Zadanie 5. (2pkt) W trójkącie równoramiennym \(ABC\), w którym \(|AC|=|BC|\), poprowadzono dwie wysokości: \(AD\) i \(CE\). Na rysunku przedstawiono ten trójkąt i zaznaczono w nim niektóre kąty.
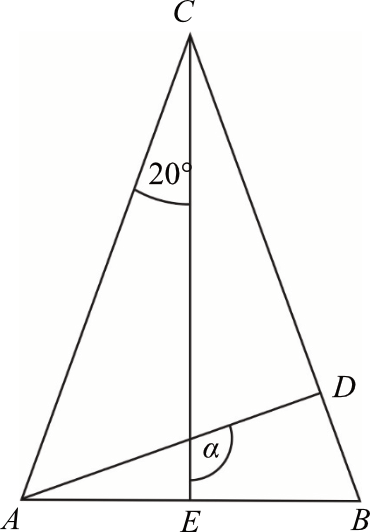
Uzasadnij, że kąt \(\alpha\) ma miarę \(110°\).
Odpowiedź
Uzasadniono, korzystając z własności trójkątów równoramiennych oraz kątów przyległych.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Zaznaczmy na rysunku kąty proste oraz oznaczmy miejsce przecięcia się wysokości jako punkt \(S\):
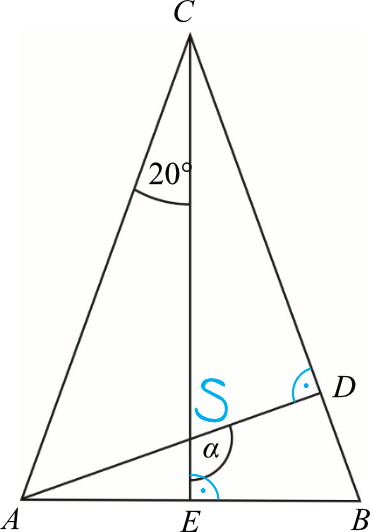
Krok 2. Obliczenie miary kąta \(ECB\) oraz \(CSD\).
Trójkąt \(ABC\) jest równoramienny, zatem wysokość \(CE\) dzieli nam kąt \(ACB\) na dwie równe części. To prowadzi nas do wniosku, że kąt \(ECB\) ma także miarę \(20°\).
Spójrzmy teraz na trójkąt \(SDC\). Znamy już dwie miary kątów w tym trójkącie, zatem kąt \(CSD\) będzie mieć miarę:
$$180°-90°-20°=70°$$
Krok 3. Obliczenie miary kąta \(\alpha\).
Kąty \(CSD\) oraz poszukiwany kąt \(\alpha\) to kąty przyległe, zatem łączna miara tych dwóch kątów jest równa \(180°\). Skoro tak, to:
$$\alpha=180°-70°=110°$$
Zadanie 6. (2pkt) Trzy proste przecinające się w sposób przedstawiony na rysunku tworzą trójkąt \(ABC\). Uzasadnij, że trójkąt \(ABC\) jest równoboczny.
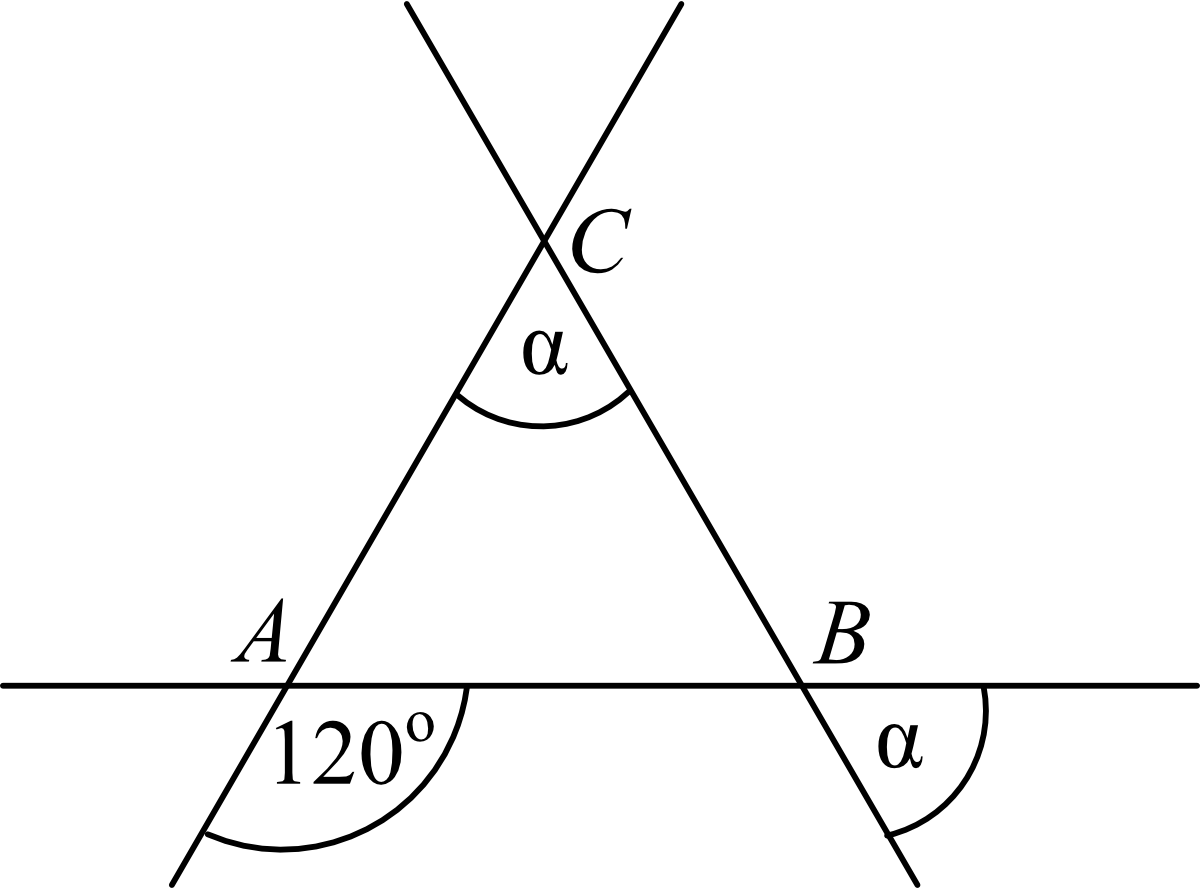
Odpowiedź
Udowodniono obliczając miary poszczególnych kątów.
Wyjaśnienie:
Krok 1. Wyznaczenie miary kąta \(CAB\).
Kąt \(CAB\) jest kątem przyległym do kąta o mierze \(120°\), a z własności kątów podobnych wiemy, że suma ich miar wynosi \(180°\). To oznacza, że:
$$|\sphericalangle CAB|=180°-120°=60°$$
Krok 2. Obliczenie miary kąta \(ABC\) oraz \(ACB\).
Zacznijmy od kąta \(ABC\). Jest on kątem wierzchołkowym do kąta \(α\) znajdującego się przy wierzchołku \(B\), zatem możemy zapisać, że:
$$|\sphericalangle ABC|=α$$
Mamy więc następującą sytuację:

O naszym trójkącie wiemy, że ma w sobie kąt \(60°\) oraz jakieś dwa kąty o jednakowej mierze \(α\). Spróbujmy zatem wyznaczyć wartość tej \(α\). Wiemy, że suma kątów w trójkącie jest równa \(180°\), zatem prawdziwą będzie równość:
$$2α+60°=180° \\
2α=120° \\
α=60°$$
Czyli:
$$|\sphericalangle ABC|=60° \\
|\sphericalangle ACB|=60°$$
Krok 3. Zakończenie dowodzenia.
Z naszej analizy wynika, że wszystkie kąty trójkąta \(ABC\) mają miarę \(60°\). Jest to charakterystyczna cecha trójkąta równobocznego, zatem udowadniając miary tych poszczególnych kątów możemy stwierdzić, że trójkąt \(ABC\) jest jak najbardziej trójkątem równobocznym.
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz miarę kąta \(\sphericalangle ABC|=60°\) (Krok 1.) oraz zapiszesz, że \(|\sphericalangle ABC|=α\) (Krok 2.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Zadanie 7. (2pkt) Trzy proste przecinają się w punktach \(A\), \(B\) i \(C\) tak, jak pokazano na rysunku. Odcinki \(AC\) i \(BC\) są równej długości. Wykaż, że miara kąta \(α\) stanowi połowę miary kąta \(β\).
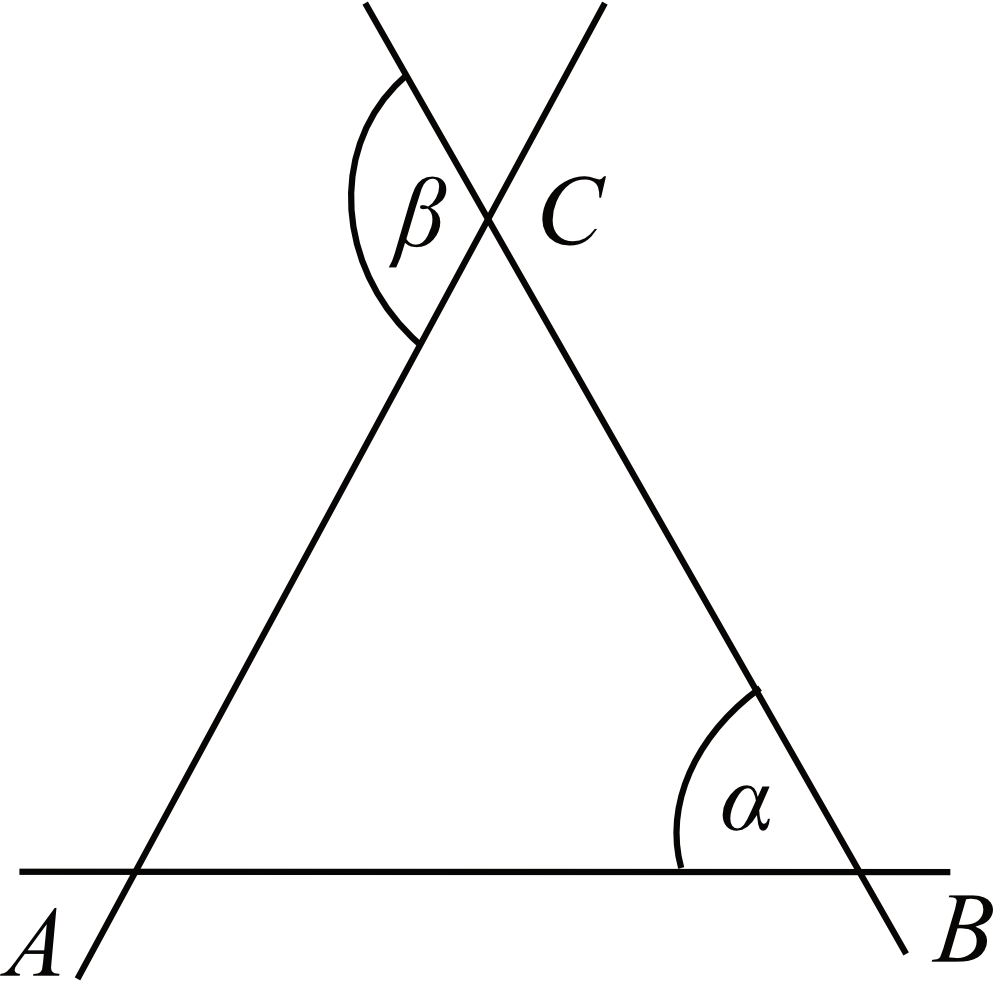
Odpowiedź
Udowodniono, korzystając z własności trójkątów równoramiennych oraz kątów przyległych.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Jeżeli odcinki \(AC\) i \(BC\) są równej długości, to trójkąt \(ABC\) jest równoramienny. W trójkątach równoramiennych kąty przy podstawie mają jednakową miarę, więc \(|\sphericalangle CAB|=\alpha\). Dodatkowo oznaczmy sobie kąt \(ACB\) jako \(\gamma\) i mamy taką oto sytuację:
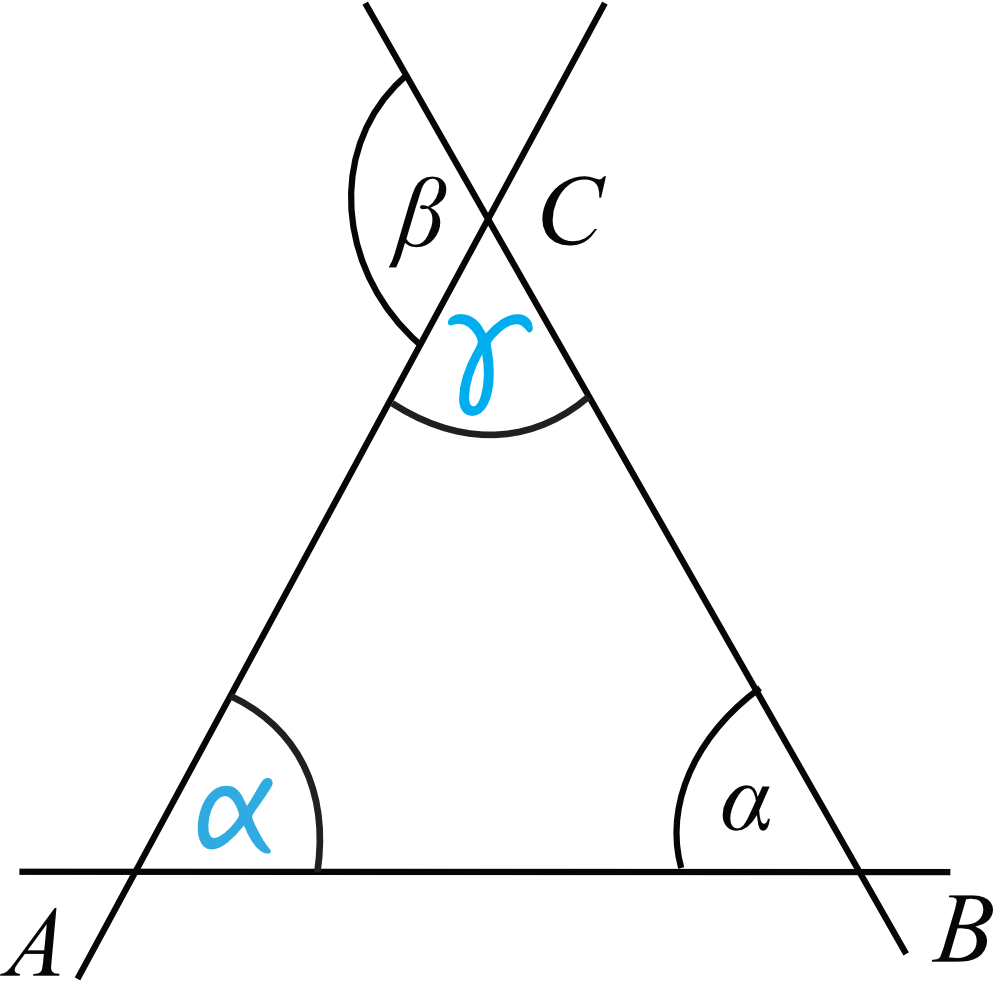
Krok 2. Zakończenie dowodzenia.
Skoro suma miar kątów w trójkącie \(ACB\) jest równa \(180°\), a kąty przy podstawie mają miarę \(\alpha\), to:
$$2\alpha+\gamma=180°$$
Do miary kąta \(ACB\) możemy też podejść z innej perspektywy. Kąt \(\beta\) oraz kąt \(ACB\) są kątami przyległymi. To prowadzi nas do wniosku, że:
$$\beta+\gamma=180°$$
Porównując teraz otrzymane dwa zapisy wyjdzie nam, że:
$$2\alpha+\gamma=\beta+\gamma \\
2\alpha=\beta \\
\alpha=\frac{1}{2}\beta$$
W ten sposób udało nam się wykazać, że kąt \(\alpha\) stanowi połowę miary kąta \(\beta\).
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy ułożysz równanie typu \(\beta=180°-2\alpha\) lub \(\alpha+\alpha+\gamma=\beta+\gamma\).
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.
Zadanie 8. (1pkt) Na rysunku przedstawiono dwa trójkąty oraz podano niektóre ich wymiary i miary kilku kątów.
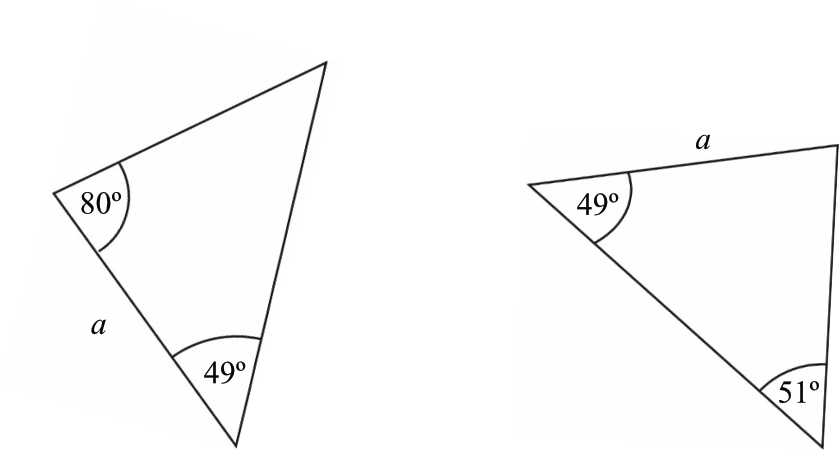
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Te trójkąty są równoramienne.
Te trójkąty są przystające.
Odpowiedź
1) FAŁSZ
2) PRAWDA
Wyjaśnienie:
Krok 1. Wyznaczenie miar kątów w trójkątach.
Znamy dwie miary kątów w każdym z trójkątów. Policzmy zatem miary brakujących kątów:
Pierwszy trójkąt:
$$180°-80°-49°=51°$$
Drugi trójkąt:
$$180°-51°-49°=80°$$
To oznacza, że obydwa trójkąty mają kąty o miarach \(49°, 51°, 80°\).
Krok 2. Ocena prawdziwości pierwszego zdania.
W trójkątach równoramiennych mamy parę kątów o jednakowej mierze (kąty przy podstawie mają tą samą miarę). W przypadku podanych trójkątów takiej sytuacji nie mamy (każdy kąt ma inną miarę), więc na pewno nie będą to trójkąty równoramienne. Zdanie jest więc fałszem.
Krok 3. Ocena prawdziwości drugiego zdania.
Wiemy już, że obydwa trójkąty mają jednakowe miary kątów: \(49°, 51°, 80°\). To oznacza, że na pewno są to trójkąty podobne (cecha kąt-kąt-kąt), ale nie wiemy jeszcze, czy są przystające (czyli czy oprócz jednakowych kątów, mają one jeszcze jednakowe długości boków).
Spójrzmy na zaznaczone odcinki \(a\). Zarówno w jednym, jak i drugim trójkącie, odcinek \(a\) jest przy kątach o mierze \(49°\) oraz \(80°\). To pozwala nam stwierdzić, że te trójkąty są faktycznie przystające (cecha kąt-bok-kąt). Zdanie jest więc prawdą.
Zadanie 9. (1pkt) Figura zacieniowana na rysunku jest równoległobokiem.
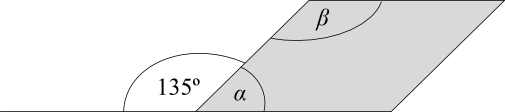
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F - jeśli jest fałszywe.
Suma miar kątów \(α\) i \(β\) wynosi \(180°\).
Kąt \(α\) ma miarę \(3\) razy mniejszą niż kąt \(β\).
Odpowiedź
1) PRAWDA
2) PRAWDA
Wyjaśnienie:
Krok 1. Ocena prawdziwości pierwszego zdania.
To zdanie jest prawdą, bo jest to po prostu jedna z własności równoległoboków. W równoległobokach kąty przy jednym ramieniu mają zawsze łącznie \(180°\).
Krok 2. Ocena prawdziwości drugiego zdania.
Obliczmy najpierw miarę kąta \(α\). Kąt \(α\) jest kątem przyległym do kąta o mierze \(135°\), a z własności kątów przyległych wiemy, że suma ich miar jest równa \(180°\). W związku z tym:
$$α=180°-135°=45°$$
Wiemy już, że suma miar kątów \(α\) i \(β\) wynosi \(180°\), zatem kąt \(β\) będzie miał miarę:
$$β=180°-45°=135°$$
To oznacza, że faktycznie kąt \(α\) ma miarę \(3\) razy mniejszą od kąta \(β\), bowiem \(135°:3=45°\).
szkoda że tak mało zadań :(( ale dzięki!
czy w zadaniu pierwszym, nie ma jeszcze symetrii po skosie?
Niestety nie ;) Pamiętaj, że nawet prostokąt nie ma tej symetrii po skosie.
a jest jakaś figura posiadająca oś symetri po skosie ?
Pewnie, że tak – chociażby kwadrat ;)
świetne zadania dziękuje za pomoc
świetne :)