Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Nanosząc na rysunek dane z treści zadania otrzymamy następującą sytuację:
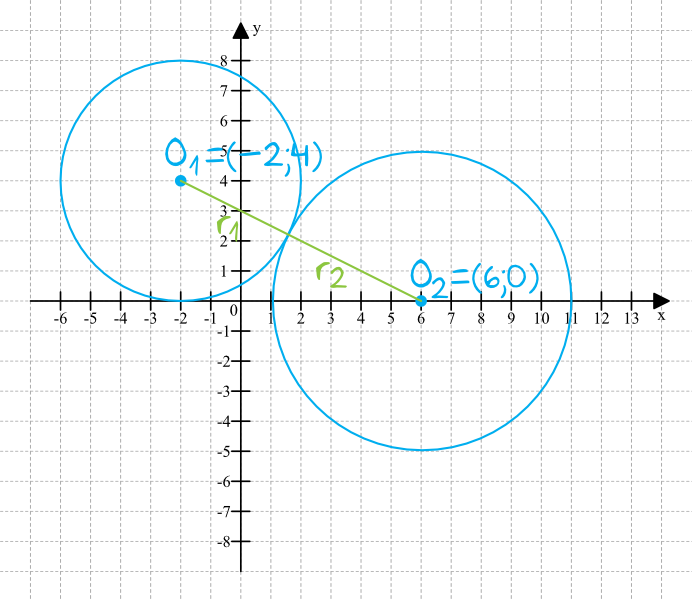
Krok 2. Obliczenie odległości między środkami okręgów.
Obliczmy odległość między środkami okręgów, czyli długość odcinka \(|O_{1}O_{2}|\). Korzystając ze wzoru na długość odcinka w układzie współrzędnych możemy zapisać, że:
$$|O_{1}O_{2}|=\sqrt{(6-(-2))^2+(0-4)^2} \\
|O_{1}O_{2}|=\sqrt{(6+2)^2+(0-4)^2} \\
|O_{1}O_{2}|=\sqrt{8^2+4^2} \\
|O_{1}O_{2}|=\sqrt{64+16} \\
|O_{1}O_{2}|=\sqrt{80} \\
|O_{1}O_{2}|=\sqrt{16\cdot5} \\
|O_{1}O_{2}|=4\sqrt{5}$$
Krok 3. Obliczenie długości promienia drugiego okręgu.
Długość drugiego okręgu jest różnicą między odcinkiem \(|O_{1}O_{2}|\) i długością krótszego okręgu, zatem:
$$r_{2}=|O_{1}O_{2}|-r_{1} \\
r_{2}=4\sqrt{5}-4 \\
r_{2}=4\cdot(\sqrt{5}-1)$$