Do wykresu funkcji wykładniczej, określonej dla każdej liczby rzeczywistej x wzorem f(x)=a^x, należy punkt P=(2,9)

Do wykresu funkcji wykładniczej, określonej dla każdej liczby rzeczywistej $x$ wzorem $f(x)=a^x$ (gdzie $a\gt0$ i $a\ne1$), należy punkt $P=(2,9)$. Oblicz $a$ i zapisz zbiór wartości funkcji $g$, określonej wzorem $g(x)=f(x)-2$.

Rozwiązanie

Krok 1. Wyznaczenie wartości $a$.
Skoro do funkcji $f(x)=a^x$ należy punkt $P=(2,9)$ to podstawiając $x=2$ oraz $y=9$ będziemy w stanie wyznaczyć wartość $a$. Zatem:
$$f(x)=a^x \\
9=a^2 \\
a=3 \quad\lor\quad a=-3$$

Wartość ujemną odrzucamy, bo z założeń wynika, że $a\gt0$. Zatem zostaje nam jedynie $a=3$.

Krok 2. Określenie zbioru wartości funkcji $g$.
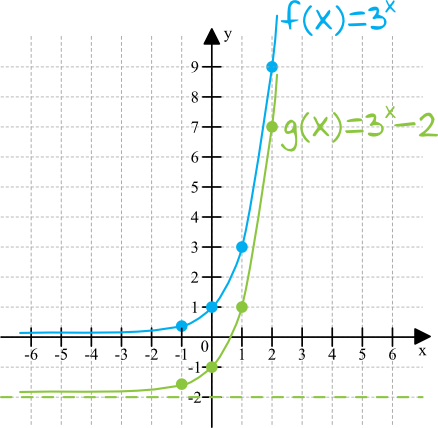
Funkcja wykładnicza w postaci $f(x)=3^x$ przyjmuje zawsze wartości dodatnie. Zbiorem wartości funkcji $f$ byłby więc przedział $(0;+\infty)$.

Nasza funkcja $g$ jest przekształceniem funkcji $f$, a dokładnie jest przesunięta o dwie jednostki w dół. To oznacza, że zbiorem wartości funkcji $g$ będzie przedział $(-2;+\infty)$.

matura z matematyki

Odpowiedź

$a=3$ oraz $y\in(-2;+\infty)$

Zadania

Do wykresu funkcji wykładniczej, określonej dla każdej liczby rzeczywistej x wzorem f(x)=a^x, należy punkt P=(2,9)

Do wykresu funkcji wykładniczej, określonej dla każdej liczby rzeczywistej \(x\) wzorem \(f(x)=a^x\) (gdzie \(a\gt0\) i \(a\ne1\)), należy punkt \(P=(2,9)\). Oblicz \(a\) i zapisz zbiór wartości funkcji \(g\), określonej wzorem \(g(x)=f(x)-2\).