Podstawą ostrosłupa prawidłowego trójkątnego \(ABCS\) jest trójkąt równoboczny \(ABC\). Wysokość \(SO\) tego ostrosłupa jest równa wysokości jego podstawy. Objętość tego ostrosłupa jest równa \(27\). Oblicz pole powierzchni bocznej ostrosłupa \(ABCS\) oraz cosinus kąta, jaki tworzą wysokość ściany bocznej i płaszczyzna podstawy ostrosłupa.
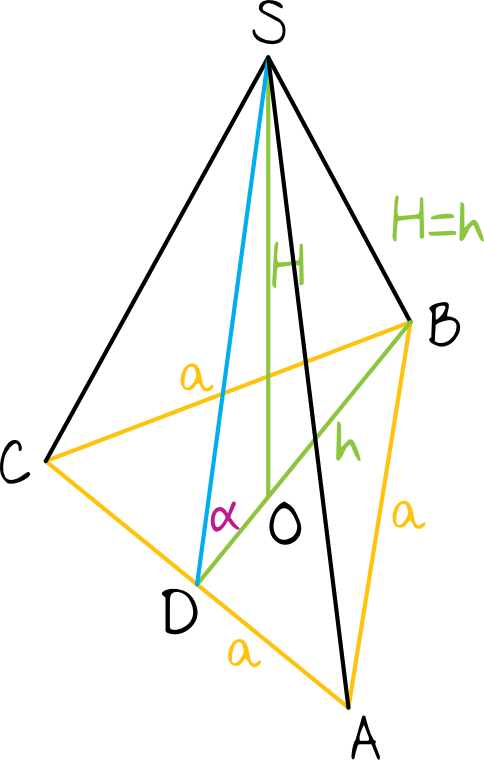
W podstawie ostrosłupa prawidłowego trójkątnego jest zawsze trójkąt równoboczny (co zresztą jest jeszcze potwierdzone w treści zadania), więc każdą długość jego krawędzi podstawy oznaczmy sobie jako niewiadomą \(a\).
Wzór na objętość ostrosłupa to \(V=\frac{1}{3}\cdot P_{p}\cdot H\). Potrzebujemy więc znać pole podstawy i wysokość bryły.
a) Pole powierzchni trójkąta równobocznego (będącego podstawą bryły) możemy zapisać jako \(P_{p}=\frac{a^2\sqrt{3}}{4}\).
b) Wysokość ostrosłupa jest zgodnie z treścią zadania równa wysokości trójkąta równobocznego znajdującego się w podstawie. Wzór na wysokość trójkąta równobocznego też jest nam znany, stąd \(H=h=\frac{a\sqrt{3}}{2}\).
c) Objętość mamy podaną w treści zadania i jest ona równa \(27\).
Podstawiając te wszystkie informacje do wzoru na objętość otrzymamy:
$$V=\frac{1}{3}\cdot P_{p}\cdot H \\
27=\frac{1}{3}\cdot\frac{a^2\sqrt{3}}{4}\cdot\frac{a\sqrt{3}}{2} \\
27=\frac{a^3\cdot\sqrt{3}\cdot\sqrt{3}}{24} \\
27=\frac{3a^3}{24} \\
27=\frac{a^3}{8} \\
a^3=27\cdot8 \\
a^3=216 \\
a=6$$
Znając już wartość długości krawędzi podstawy możemy zapisać wysokość ostrosłupa (i tym samym wysokość trójkąta równobocznego znajdującego się w podstawie) w formie konkretnej liczby:
$$H=\frac{a\sqrt{3}}{2} \\
H=\frac{6\sqrt{3}}{2} \\
H=3\sqrt{3}$$
Aby obliczyć pole powierzchni ściany bocznej ostrosłupa (bo o nią proszą nas w zadaniu) potrzebujemy znać długość podstawy (tą już mamy wyliczoną) oraz wysokość ściany bocznej – i to właśnie ją teraz sobie policzymy.
Do wyznaczenia wysokości ściany bocznej posłużymy się trójkątem prostokątnym \(DOS\). Odcinek \(DO\) zgodnie z własnościami trójkąta równobocznego stanowi \(\frac{1}{3}\) długości wysokości trójkąta, czyli:
$$|DO|=\frac{1}{3}h \\
|DO|=\frac{1}{3}\cdot3\sqrt{3} \\
|DO|=\sqrt{3}$$
Z Twierdzenia Pitagorasa wynika, że:
$$|DO|^2+|OS|^2=|DS|^2 \\
(\sqrt{3})^2+(3\sqrt{3})^2=|DS|^2 \\
3+9\cdot3=|DS|^2 \\
|DS|^2=30 \\
|DS|=\sqrt{30}$$
Pamiętając o tym, że mamy trzy trójkąty w ścianach bocznych, to pole powierzchni bocznej jest równe:
$$P_{b}=\frac{1}{2}\cdot a\cdot|DS|\cdot3 \\
P_{b}=\frac{1}{2}\cdot 6\cdot\sqrt{30}\cdot3 \\
P_{b}=9\sqrt{30}$$
Zgodnie z treścią zadania musimy jeszcze podać wartość cosinusa jaki tworzą wysokość ściany bocznej i płaszczyzna podstawy ostrosłupa. W naszym przypadku będzie to kąt \(SDB\):
$$cos\sphericalangle SDB=\frac{|DO|}{|DS|} \\
cos\sphericalangle SDB=\frac{\sqrt{3}}{\sqrt{30}}$$
Usuwając jeszcze niewymierność z mianownika otrzymamy:
$$cos\sphericalangle SDB=\frac{\sqrt{3}\cdot\sqrt{30}}{\sqrt{30}\cdot\sqrt{30}}=\frac{\sqrt{90}}{30}= \\
=\frac{\sqrt{9\cdot10}}{30}=\frac{3\sqrt{10}}{30}=\frac{\sqrt{10}}{10}$$
\(P_{b}=9\sqrt{30}\) oraz \(cosα=\frac{\sqrt{10}}{10}\)

