Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Sytuacja z treści zadania będzie wyglądać następująco:
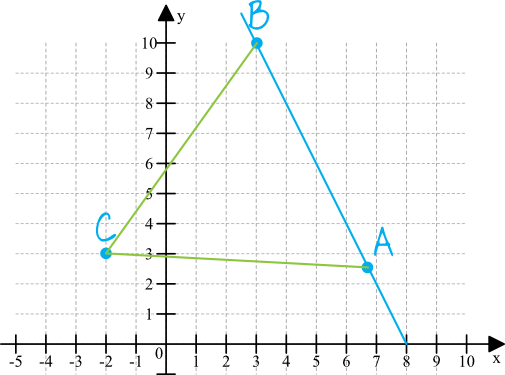
Krok 2. Zapisanie równania wynikającego z równej długości ramion.
Skoro trójkąt \(ABC\) jest równoramienny, to długość odcinka \(AC\) musi być równa długości \(BC\). Korzystając ze wzoru na długość odcinka moglibyśmy więc zapisać, że:
$$|AC|=|BC| \\
\sqrt{(x_{C}-x_{A})^2+(y_{C}-y_{A})^2}=\sqrt{(x_{C}-x_{B})^2+(y_{C}-y_{B})^2} \\
(x_{C}-x_{A})^2+(y_{C}-y_{A})^2=(x_{C}-x_{B})^2+(y_{C}-y_{B})^2$$
Teraz do tego równania musimy podstawić współrzędne z treści zadania. Oczywiście brakuje nam współrzędnych punktu \(A\) (to właśnie ich szukamy), ale i tutaj możemy już dokonać ważnej obserwacji. Skoro prosta \(y=-2x+16\) przechodzi przez punkt \(A\), to znaczy, że współrzędna \(y_{A}\) da się opisać równaniem \(-2x+16\). Moglibyśmy nawet zapisać, że współrzędne punktu \(A\) to \(A=(x;-2x+16)\). Podstawiając zatem te współrzędne oraz współrzędne \(B=(3,10)\) i \(C=(-2,3)\), otrzymamy:
$$(-2-x)^2+(3-(-2x+16))^2=(-2-3)^2+(3-10)^2 \\
(-2-x)^2+(3+2x-16)^2=(-5)^2+(-7)^2 \\
(-2-x)^2+(2x-13)^2=25+49 \\
4+4x+x^2+4x^2-52x+169=74 \\
5x^2-48x+99=0$$
Krok 3. Rozwiązanie powstałego równania kwadratowego.
Powstało nam równanie kwadratowe w postaci ogólnej, zatem skorzystamy z niezawodnej delty:
Współczynniki: \(a=5,\;b=-48,\;c=99\)
$$Δ=b^2-4ac=(-48)^2-4\cdot5\cdot99=2304-1980=324 \\
\sqrt{Δ}=\sqrt{324}=18$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-48)-18}{2\cdot5}=\frac{48-18}{10}=\frac{30}{10}=3 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-48)+18}{2\cdot5}=\frac{48+18}{10}=\frac{66}{10}=6,6$$
Krok 4. Zapisanie współrzędnych punktu \(A\).
Otrzymaliśmy dwie możliwości współrzędnej \(x\) punktu \(A\). Ta wartość może być równa \(x=3\) oraz \(x=6,6\). Pierwszy przypadek musimy odrzucić, a to dlatego, że \(x=3\) to współrzędna punktu \(B\) (który przecież leży na tej samej prostej co punkt \(A\)). Punkty \(A\) oraz \(B\) nie mogą się pokrywać, więc zostaje nam, że \(x=6,6\).
Skoro tak, to obliczmy teraz współrzędną \(y\). W tym celu wystarczy podstawić \(x=6,6\) do równania prostej \(y=-2x+16\), zatem:
$$y=-2\cdot6,6+16 \\
y=-13,2+16 \\
y=2,8$$
To oznacza, że \(A=(6,6;2,8)\).
Krok 5. Obliczenie pola powierzchni trójkąta.
Na sam koniec musimy obliczyć pole powierzchni tego trójkąta. Nie będzie to trudne, bo mając współrzędne wszystkich wierzchołków tej figury, możemy skorzystać ze specjalnego wzoru z tablic:
$$P=\frac{1}{2}|(x_{B}-x_{A})(y_{C}-y_{A})-(y_{B}-y_{A})(x_{C}-x_{A})| \\
P=\frac{1}{2}|(3-6,6)\cdot(3-2,8)-(10-2,8)\cdot(-2-6,6)| \\
P=\frac{1}{2}|(-3,6)\cdot(0,2)-(7,2)\cdot(-8,6)| \\
P=\frac{1}{2}|(-0,72)-(-61,92)| \\
P=\frac{1}{2}|-0,72+61,92| \\
P=\frac{1}{2}|61,2| \\
P=\frac{1}{2}\cdot61,2 \\
P=30,6$$