Dany jest trójkąt prostokątny o długościach boków \(a,b,c\), gdzie \(a\lt b\lt c\). Obracając ten trójkąt wokół prostej zawierającej dłuższą przyprostokątną o kąt \(360°\) otrzymujemy bryłę, której objętość jest równa:
\(V=\frac{1}{3}a^2bπ\)
\(V=a^2bπ\)
\(V=\frac{1}{3}b^2aπ\)
\(V=a^2π+πac\)
Rozwiązanie:
W trójkącie najdłuższym bokiem jest przeciwprostokątna, więc ją od razu możemy oznaczyć jako bok \(c\). Skoro obrót jest dokonywany wzdłuż dłużej przyprostokątnej, to stożek będzie wyglądał mniej więcej w ten sposób:
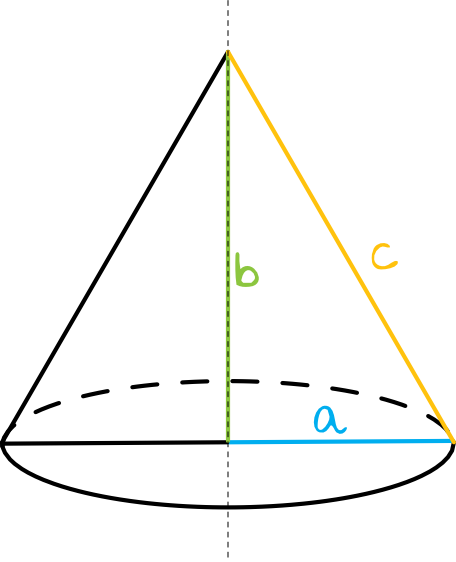
Standardowy wzór na objętość stożka to:
$$V=\frac{1}{3}πr^2\cdot H$$
W naszym przypadku \(r=a\) oraz \(H=b\), zatem poszukiwanym wzorem jest:
$$V=\frac{1}{3}a^2bπ$$
Odpowiedź:
A. \(V=\frac{1}{3}a^2bπ\)

