Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Opisana w zadaniu sytuacja będzie wyglądać mniej więcej w ten sposób:
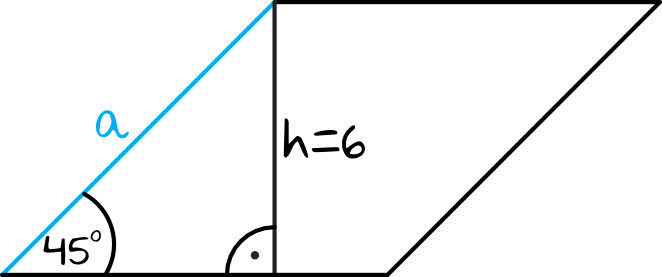
Krok 2. Obliczenie długości boku rombu.
Spójrzmy na zaznaczony na rysunku trójkąt prostokątny. Jest to klasyczny trójkąt o kątach \(45°,45°,90°\). Jedną z własności takich trójkątów jest to, że jeżeli przyprostokątne mają długość \(a\), to przeciwprostokątna ma długość \(a\sqrt{2}\). W naszym przypadku przyprostokątna ma długość \(h=6\), zatem przeciwprostokątna (która jest bokiem rombu) będzie miała długość \(a=6\sqrt{2}\).
Krok 3. Obliczenie pola rombu.
Znając długość boku rombu oraz jego wysokość możemy już bez przeszkód obliczyć pole naszej figury:
$$P=a\cdot h \\
P=6\sqrt{2}\cdot6 \\
P=36\sqrt{2}[cm^2]$$