Wykres funkcji liniowej jest linią prostą (co sugeruje zresztą sama nazwa funkcji). W tym temacie powiemy sobie jak rysować wykresy funkcji liniowej oraz jakie kluczowe informacje z takiego wykresu możemy odczytać.
Jak narysować wykres funkcji liniowej?
Jedną z głównych własności wykresu funkcji liniowej jest to, że do jej narysowania wystarczy znać współrzędne dwóch punktów. Przez takie dwa konkretne punkty przechodzić będzie tylko jedna prosta. Spójrzmy jak to będzie wyglądać w praktyce.
Na początek obliczymy współrzędne dwóch punktów przez które będzie przechodzić nasza prosta. Zrobimy to podstawiając do wzoru funkcji dwa wybrane przez siebie argumenty. Nie ma sensu podstawiać jakichś dużych liczb, zazwyczaj najlepszym pomysłem jest podstawienie argumentów typu \(x=0\), \(x=1\), \(x=2\), czy też \(x=3\). Warto też zauważyć, że im dalej będą te punkty od siebie położone tym nasz rysunek będzie dokładniejszy.
Dla \(x=0\) otrzymamy:
$$y=2\cdot0+1 \\
y=0+1 \\
y=1$$
To oznacza, że wykres funkcji \(y=2x+1\) na pewno przechodzi przez punkt o współrzędnych \((0;1)\).
Dla \(x=1\) otrzymamy:
$$y=2\cdot1+1 \\
y=2+1 \\
y=3$$
To oznacza, że wykres funkcji \(y=2x+1\) na pewno przechodzi przez punkt o współrzędnych \((1;3)\).
Znamy już więc współrzędne dwóch punktów, zatem możemy zaznaczyć je w układzie współrzędnych i narysować odpowiednią prostą:
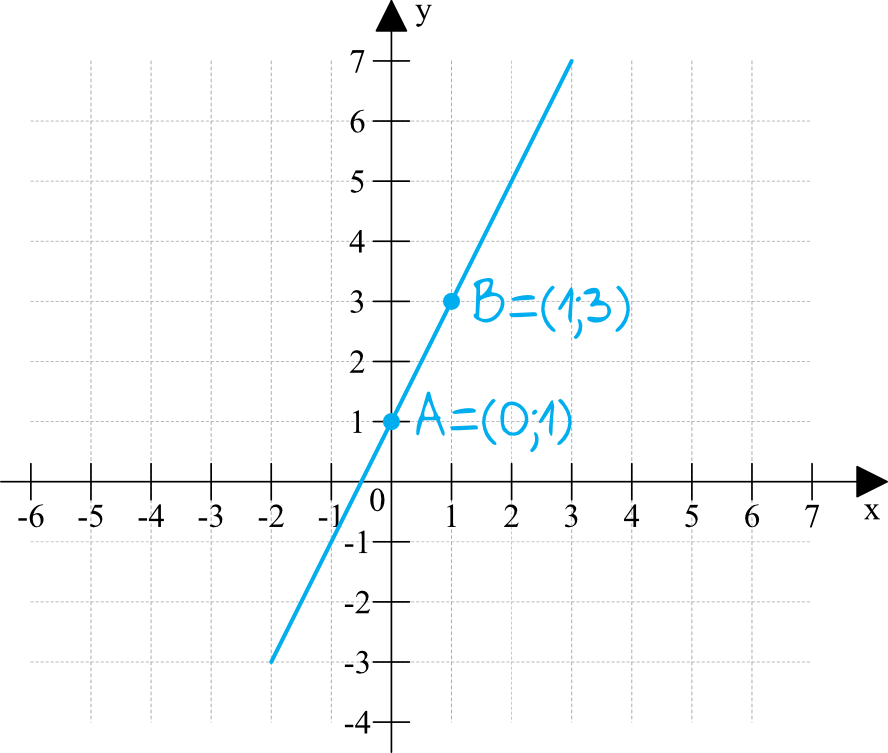
Sytuacja jest bardzo podobna do poprzedniej, zatem sposób postępowania jest identyczny i zaczynamy od wyznaczenia współrzędnych dwóch punktów:
Dla \(x=0\) otrzymamy:
$$y=-2\cdot0+4 \\
y=0+4 \\
y=4$$
To oznacza, że wykres tej funkcji przechodzi przez punkt o współrzędnych \((0;4)\).
Dla \(x=3\) otrzymamy:
$$y=-2\cdot3+4 \\
y=-6+4 \\
y=-2$$
To oznacza, że wykres tej funkcji przechodzi przez punkt o współrzędnych \((3;-2)\).
Znając współrzędne dwóch punktów możemy bez przeszkód narysować wzór funkcji:
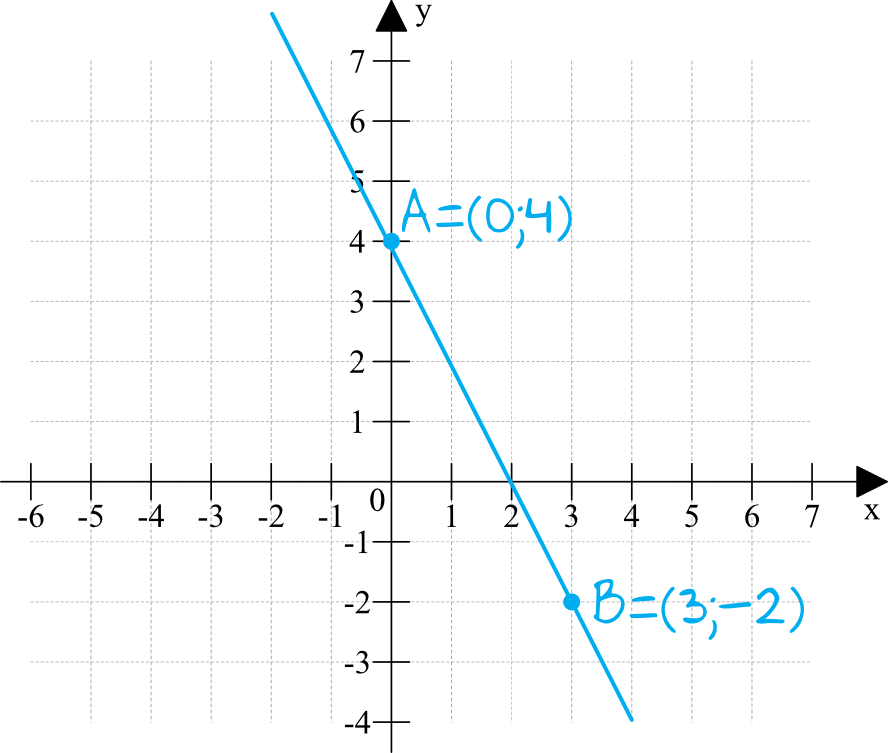
Dlaczego w pierwszym przykładzie wzięliśmy do obliczeń \(x=0\) oraz \(x=1\), a w drugim \(x=0\) oraz \(x=3\)? Możemy wziąć dowolne argumenty, więc mamy pełną swobodę działania. Jednak jak potrzebujemy narysować wykres funkcji dość dokładny, to właśnie lepiej jest wziąć ten drugi punkt nieco bardziej oddalony od pierwszego, tak jak to miało miejsce w drugim przykładzie.
Współczynnik kierunkowy \(a\)
Rysowanie funkcji liniowych nie jest więc trudne, dlatego przejdźmy do kolejnego zagadnienia związanego z wykresem funkcji liniowej. Jak przyjrzymy się funkcjom narysowanym w powyższych przykładach to zauważymy, że są pewne rzeczy które je różnią i to dość mocno. Taką główną różnicą jest to, że wykres pierwszej funkcji jest rosnący, a wykres drugiej funkcji jest malejący. Co sprawia, że tak się dzieje? Żeby rozwikłać tę zagadkę musimy sobie przypomnieć, że wzór każdej funkcji liniowej możemy opisać jako \(y=ax+b\). O tym czy funkcja rośnie czy maleje decyduje tak zwany współczynnik kierunkowy \(a\), czyli liczba stojąca przed iksem.
• Gdy \(a\gt0\) to funkcja liniowa jest rosnąca i tak właśnie było w pierwszym przykładzie, gdzie \(a=2\).
• Gdy \(a\lt0\) to funkcja liniowa jest malejąca i tak właśnie było w drugim przykładzie, gdzie \(a=-2\).
• Gdy \(a=0\) to funkcja liniowa jest stała.
Współczynnik \(b\)
Ale to nie koniec ciekawych wniosków. Spójrzmy w tych dwóch powyższych przykładach na miejsce przecięcia się wykresu z osią igreków. Ma ono wiele wspólnego ze współczynnikiem \(b\) (czyli wyrazem wolnym) naszej funkcji. W pierwszej funkcji wykres przeciął oś igreków dla \(y=1\), a funkcja ta miała współczynnik \(b=1\). Podobnie było w przypadku drugiej funkcji, tutaj oś została przecięta dla \(y=4\), a współczynnik \(b\) tej drugiej funkcji był równy \(b=4\).
Miejsce zerowe funkcji liniowej
Miejsce zerowe funkcji liniowej to argument dla którego funkcja przyjmuje wartość równą \(0\). Jeżeli więc funkcja ma miejsce zerowe np. \(x=3\), to taka informacja oznacza, że dla argumentu \(x=3\) ta funkcja przyjmuje wartość równą \(0\). Obrazowo rzecz ujmując będziemy mogli powiedzieć, że w takiej sytuacji wykres funkcji będzie przechodzić przez punkt o współrzędnych \((3;0)\).
Spójrzmy na przykładowe zadania związane z własnościami wykresów funkcji:
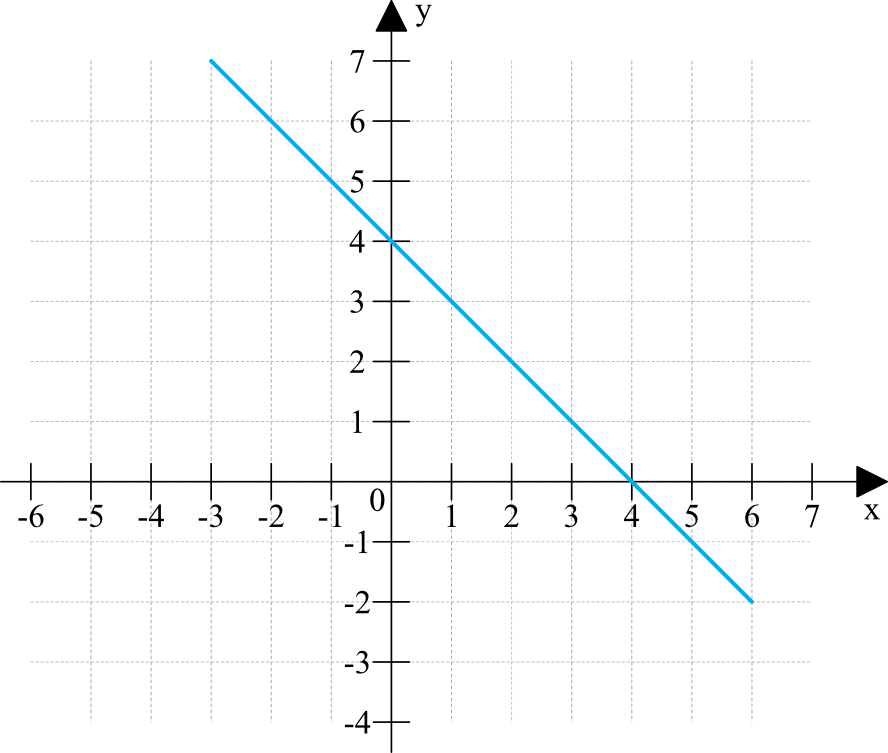
Współczynnik \(a\) wynika z kierunku naszej prostej. Prosta jest malejąca, zatem możemy powiedzieć, że \(a\lt0\).
Współczynnik \(b\) odczytamy spoglądając na miejsce przecięcia się wykresu z osią igreków. Widzimy wyraźnie, że funkcja przecina oś igreków dla dodatnich wartości, zatem \(b\gt0\).
Możemy tutaj narysować sobie układ współrzędnych i zaznaczyć miejsca wskazane w treści zadania:
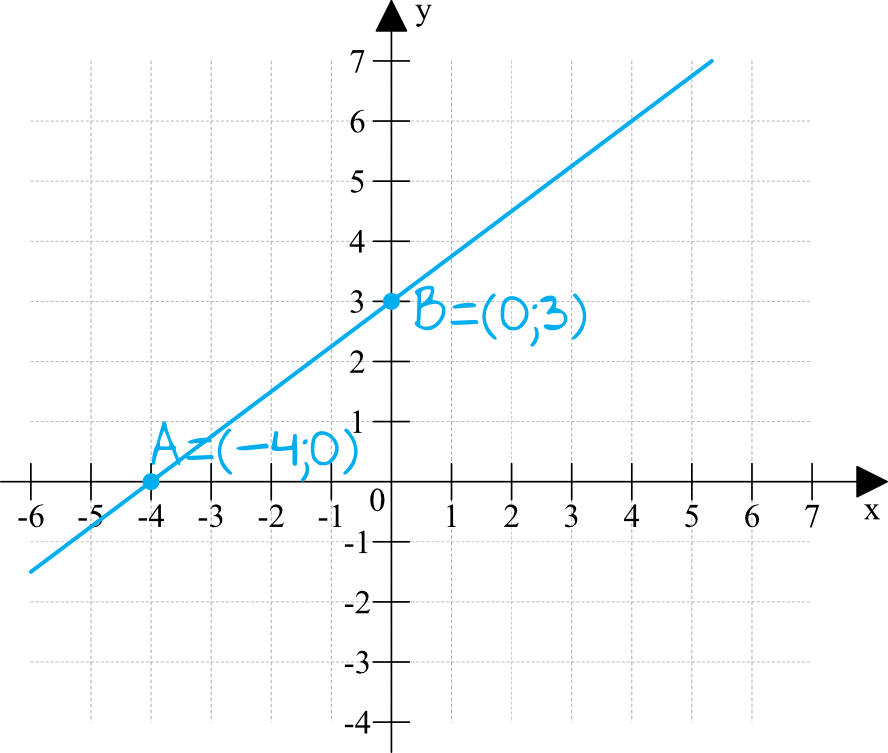
Z takiego rysunku wyraźnie widać, że funkcja jest rosnąca.
