Rozwiązanie
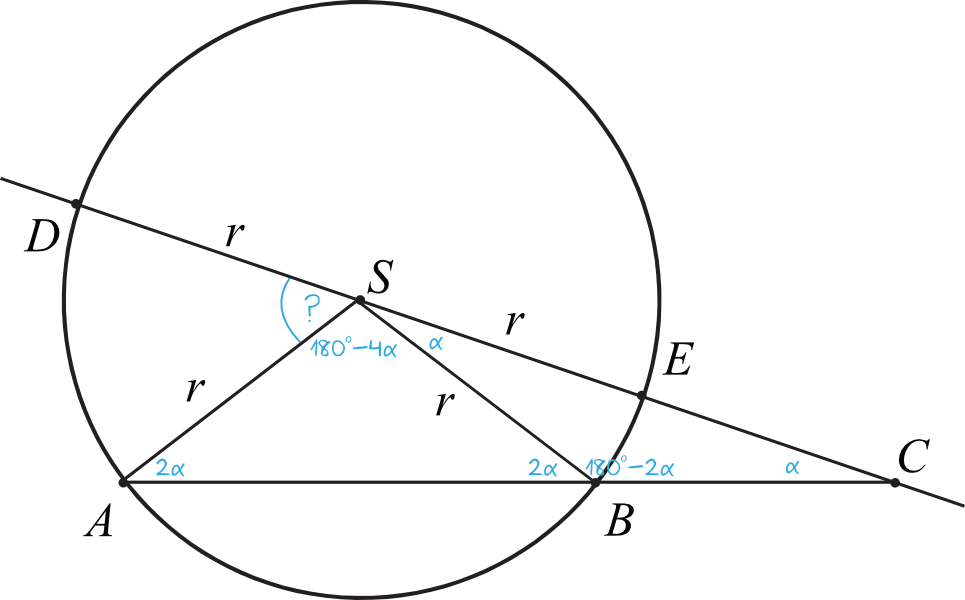
Krok 1. Wyznaczenie miary kąta \(SBC\).
Spójrzmy na trójkąt \(SBC\). Wiemy, że jest to trójkąt równoramienny, bo z treści zadania wynika, że \(SB=BC\). Skoro tak, to kąty przy podstawie tego trójkąta mają identyczną miarę. Jeżeli więc kąt \(ACS\) (czyli tak jakby \(BCS\)) ma miarę \(α\), to kąt \(BSC\) ma także miarę równą \(α\).
To z kolei oznacza, że skoro w trójkącie suma kątów ma być równa \(180°\), to kąt \(SBC\) ma miarę:
$$|\sphericalangle SBC|=180°-α-α=180°-2α$$
Krok 2. Wyznaczenie miary kąta \(ABS\).
Kąt \(ABS\) i kąt \(SBC\) to kąty przyległe, których łączna miara musi mieć w takim razie \(180°\). Skoro \(|\sphericalangle SBC|=180°-2α\), to znaczy że kąt \(ABS\) musi mieć miarę równą \(2α\). Jeżeli ktoś tego nie dostrzega, to możemy to rozpisać w taki sposób:
$$|\sphericalangle ABS|=180°-|\sphericalangle SBC| \\
|\sphericalangle ABS|=180°-(180°-2α) \\
|\sphericalangle ABS|=180°-180°+2α \\
|\sphericalangle ABS|=2α$$
Krok 3. Obliczenie miary kąta \(ASB\).
Teraz spójrzmy na trójkąt \(ABS\). To także trójkąt równoramienny (ramiona \(AS\) oraz \(BS\) są promieniami okręgu), zatem tutaj też kąty przy podstawie mają jednakową miarę. Skoro więc \(|\sphericalangle ABS|=2α\) to i \(|\sphericalangle SAB|=2α\).
To z kolei oznacza, że trzeci kąt w tym trójkącie, czyli kąt \(ASB\) będzie miał miarę:
$$|\sphericalangle ASB|=180°-2α-2α=180°-4α$$
Krok 4. Obliczenie miary kąta \(ASD\).
Suma kątów \(ASD\), \(ASB\) oraz \(BSC\) musi nam dać łącznie \(180°\). Już ustaliliśmy, że \(|\sphericalangle ASB|=180°-4α\) oraz \(|\sphericalangle ASB|=α\). Szukamy miary kąta \(ASD\) zatem:
$$|\sphericalangle ASD|=180°-|\sphericalangle ASB|-|\sphericalangle BSC| \\
|\sphericalangle ASD|=180°-(180°-4α)-α \\
|\sphericalangle ASD|=180°-180°+4α-α \\
|\sphericalangle ASD|=3α$$
Udało nam się udowodnić, że \(|\sphericalangle ASD|=3α\), zatem dowód możemy uznać za zakończony.