W trapezie ABCD (AB||CD) przekątne AC i BD przecinają się w punkcie O takim, że AO:OC=5:1

W trapezie $ABCD$ ($AB||CD$) przekątne $AC$ i $BD$ przecinają się w punkcie $O$ takim, że $|AO|:|OC|=5:1$. Pole trójkąta $AOD$ jest równe $10$. Uzasadnij, że pole trapezu $ABCD$ jest równe $72$.

Rozwiązanie:

Krok 1. Obliczenie pola trójkąta $OCD$ oraz $ACD$.

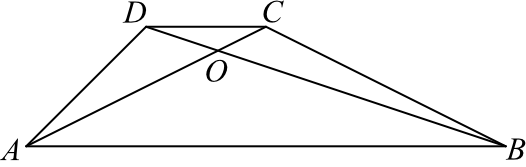
Spójrzmy na trójkąt $ACD$, możemy go sobie nawet wyodrębnić z całego rysunku i naszkicować:

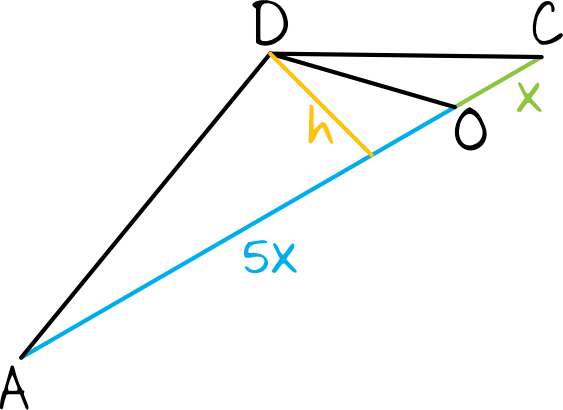
Gdybyśmy chcieli obliczyć pole trójkąta $OCD$ (którego pola powierzchni szukamy), to byłoby to:
$$P_{OCD}=\frac{1}{2}\cdot x\cdot h \\
P_{OCD}=0,5x\cdot h$$

Gdybyśmy chcieli obliczyć pole trójkąta $AOD$ (którego pole powierzchni znamy), to byłoby to:
$$P_{AOD}=\frac{1}{2}\cdot5x\cdot h \\
P_{AOD}=2,5x\cdot h$$

Widzimy wyraźnie, że pole trójkąta $AOD$ jest pięciokrotnie większe od trójkąta $OCD$. Skoro więc $P_{AOD}=10$, to $P_{OCD}=10:5=2$.

Tym samym możemy wyznaczyć pole trójkąta $ACD$:
$$P_{ACD}=P_{AOD}+P_{OCD}=10+2=12$$

Krok 2. Ustalenie podobieństwa trójkątów $ABO$ i $OCD$.

Ale to nie wszystko, bo znamy też skalę podobieństwa tych trójkątów. Skoro odcinek $AO$ jest pieć razy dłuższy od odcinka $OC$, to skala podobieństwa wynosi $k=5$. Z własności figur podobnych wiemy, że jeśli boki pierwszej figury podobnej są $k$ razy większe od boków figury drugiej, to pole powierzchni pierwszej figury jest $k^2$ większe. W naszym przypadku oznaczać to będzie, że pole trójkąta $ABO$ jest $5^2=25$ razy większe od pola trójkąta $OCD$, czyli:
$$P_{ABO}=25\cdot2=50$$

Krok 3. Obliczenie pola powierzchni trójkąta $OBC$.

Spójrzmy na duże trójkąty $ABD$ oraz $ABC$. Ich miary pól powierzchni muszą być sobie równe, bo obydwa trójkąty mają tą samą podstawę $|AB|$ oraz tą samą wysokość (która jest wysokością trapezu). Pole trójkąta $ABD$ możemy obliczyć bardzo szybko:
$$P_{ABD}=P_{ABO}+P_{AOD} \\
P_{ABD}=50+10 \\
P_{ABD}=60$$

Skoro tak, to także $P_{ABC}=60$, zatem możemy wyznaczyć pole trójkąta $OBC$:
$$P_{ABC}=P_{ABO}+P_{OBC} \\
60=50+P_{OBC} \\
P_{OBC}=10$$

Krok 4. Obliczenie pola trapezu.

Obliczyliśmy wartości czterech mniejszych trójkątów wchodzących w skład trapezu, więc pole trapezu będzie sumą naszych wszystkich wyników:
$$P_{ABCD}=P_{ABO}+P_{AOD}+P_{OBC}+P_{OCD} \\
P_{ABCD}=50+10+10+2 \\
P_{ABCD}=72$$

Wynik wyszedł nam taki sam jak w treści zadania, tak więc dowód możemy uznać za zakończony.

Odpowiedź:

Udowodniono wykorzystując własności trójkątów podobnych.

Zadania

W trapezie ABCD (AB||CD) przekątne AC i BD przecinają się w punkcie O takim, że AO:OC=5:1

W trapezie \(ABCD\) (\(AB||CD\)) przekątne \(AC\) i \(BD\) przecinają się w punkcie \(O\) takim, że \(|AO|:|OC|=5:1\). Pole trójkąta \(AOD\) jest równe \(10\). Uzasadnij, że pole trapezu \(ABCD\) jest równe \(72\).