Dane są proste o równaniach \(y=x+2\) oraz \(y=-3x+b\), które przecinają się w punkcie leżącym na osi \(Oy\) układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi \(Ox\).
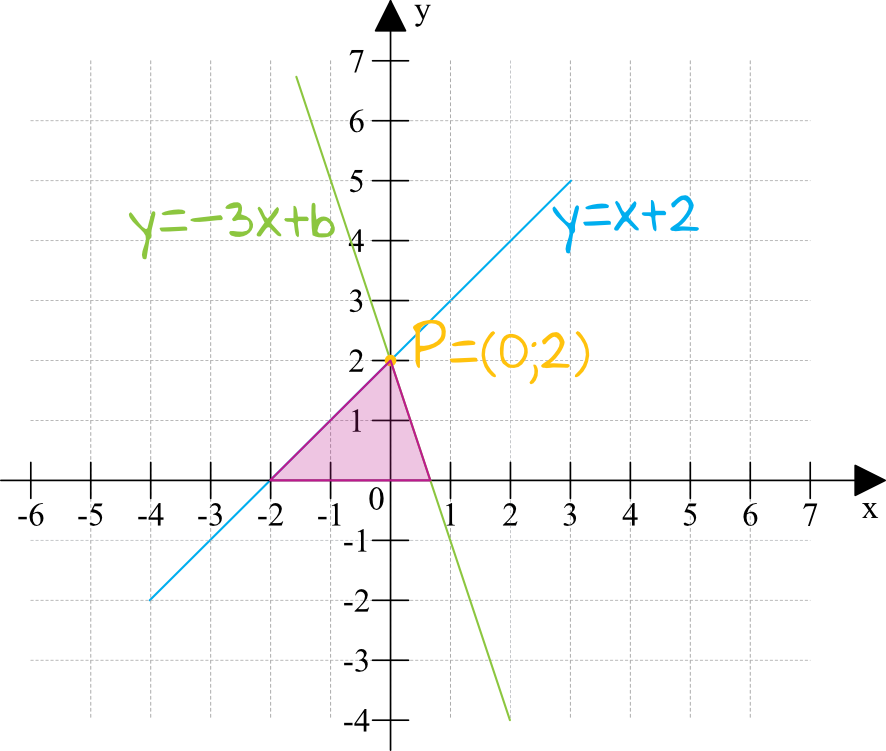
Jedna z tych prostych jest rosnąca (bo ma dodatni współczynnik kierunkowy \(a=1\)), a druga jest malejąca (bo jej współczynnik kierunkowy \(a=-3\)). Bardzo ważną informacją jest to, że te dwie proste przecinają się w punkcie \(P=(0,2)\). To automatycznie oznacza, że obydwie proste mają współczynnik \(b=2\).
Obliczmy sobie miejsca w których te dwie proste przecinają się z osią \(Ox\) (czyli miejsca zerowe). Znajomość tych współrzędnych przyda nam się do wyznaczania długości podstawy trójkąta. Aby obliczyć miejsca zerowe wystarczy przyrównać \(x+2\) oraz \(-3x+2\) do zera, zatem:
I prosta: \(x_{1}+2=0 \Rightarrow x_{1}=-2\)
II prosta: \(-3x_{2}+2=0 \Rightarrow x_{2}=\frac{2}{3}\)
Za pomocą obliczonych przed chwilą współrzędnych możemy określić długość podstawy trójkąta:
$$a=|x_{2}-x_{1}|=\left|\frac{2}{3}-(-2)\right|=2\frac{2}{3}$$
Wysokość trójkąta znamy, bo pokrywa się ona z osią \(Oy\), a więc bez problemu możemy określić że \(h=2\). Długość podstawy obliczyliśmy sobie przed chwilą i wyszło, że \(a=2\frac{2}{3}\). Zatem pole tego trójkąta jest równe:
$$P=\frac{1}{2}\cdot a\cdot h \\
P=\frac{1}{2}\cdot2\frac{2}{3}\cdot2 \\
P=2\frac{2}{3}$$
\(P=2\frac{2}{3}\)


Przydatne, polecam!