Dane są dwie funkcje określone dla wszystkich liczb rzeczywistych \(x\) wzorami \(f(x)=-5x+1\) oraz \(g(x)=5^x\). Liczba punktów wspólnych wykresów tych funkcji wynosi:
\(3\)
\(2\)
\(1\)
\(0\)
Rozwiązanie:
Krok 1. Obliczenie wartości kilku argumentów obydwu funkcji.
Spróbujmy obliczyć wartości kilku charakterystycznych argumentów, tak aby móc za chwilę wykonać szkic rysunku obydwu funkcji:
$$f(0)=-5\cdot0+1=0+1=1 \\
f(1)=-5\cdot1+1=-5+1=-4 \\
f(-1)=-5\cdot(-1)+1=5+1=6 \\
\text{oraz} \\
g(0)=5^0=1 \\
g(1)=5^1=5 \\
g(-1)=5^{-1}=\frac{1}{5}$$
Krok 2. Sporządzenie szkicu wykresów obydwu funkcji.
Nanieśmy wyznaczone przed chwilą punkty i sprawdźmy ile punktów wspólnych będą mieć wykresy tych funkcji.
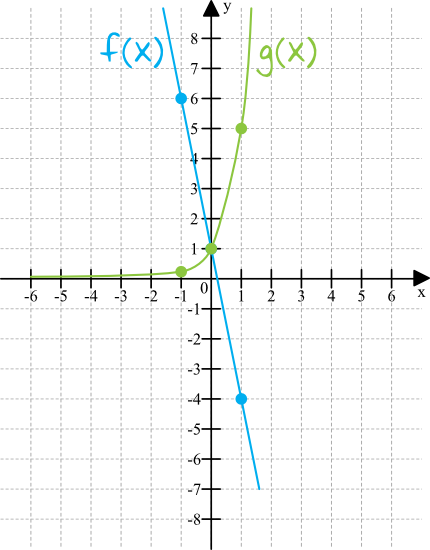
Widzimy wyraźnie, że te dwie funkcje mają jeden punkt wspólny i jest to punkt o współrzędnych \((0;1)\).
Odpowiedź:
C. \(1\)


Bardzo pomocne rozwiązanie. Dziękuję bardzo! :)