Ciąg \((a_{n})\) jest określony wzorem \(a_{n}=(n+3)(n-5)\) dla \(n\ge1\). Liczba ujemnych wyrazów tego ciągu jest równa:
Chcąc sprawdzić dla jakich wartości \(n\) ciąg przyjmuje wartości ujemne musimy rozwiązać następującą nierówność kwadratową:
$$(n+3)(n-5)\lt0$$
Ta nierówność jest zapisana w postaci iloczynowej, zatem w bardzo łatwy sposób wyznaczymy jej miejsca zerowe – wystarczy przyrównać wartość każdego z nawiasów do zera:
$$n+3=0 \quad\lor\quad n-5=0 \\
n=-3 \quad\lor\quad n=5$$
Ramiona paraboli będą skierowane do góry, bo przed przed \(n\) nie stoi żaden znak minusa. Zaznaczamy wyznaczone przed chwilą miejsca zerowe (kropki będą niezamalowane, bo w nierówności wystąpił znak \(\lt\)) i szkicujemy wykres paraboli.
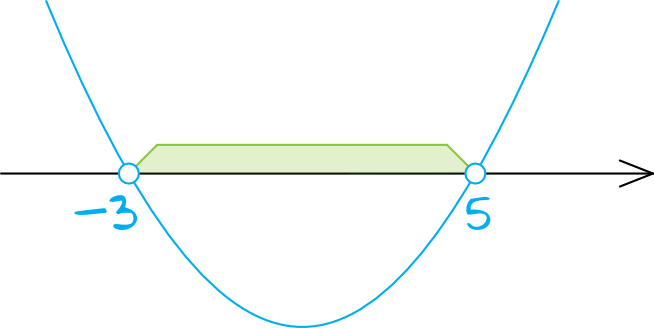
Interesują nas wartości ujemne, czyli znajdujące się pod osią, a więc rozwiązaniem naszej nierówności jest przedział \(x\in(-3;5)\).
Teraz musimy się zastanowić co ten wynik oznacza i jaka jest odpowiedź na nasze zadanie, bowiem pytają nas o to ile jest wyrazów ujemnych w tym ciągu. Musimy więc w otrzymanym rozwiązaniu uwzględnić jeszcze założenie wynikające z własności ciągów, czyli że \(n\) jest liczbą naturalną dodatnią. W związku z tym rozwiązaniami które nas interesują są jedynie:
$$x\in{1,2,3,4}$$
(Piątki nie uwzględniamy, bo nawias nie był domknięty).
To oznacza, że są tylko cztery wyrazy tego ciągu, które przyjmują ujemną wartość.
B. \(4\)


Dlaczego w treści zadania jest n>=1 a potem n=-3?
No i właśnie dlatego potem odrzucamy te ujemne wyniki, bo n musi być liczbą naturalną ;)
nie rozumiem, które liczby znajdują się pod osia?
Zobacz – nad osią masz dwa ramiona, a pod osią masz ten „dołek”. I ten dołek jest od argumentów od -3 aż do 5 i tak właśnie odczytujemy rozwiązania :)