Przekształcenia wykresów funkcji

Przekształcenia wykresów funkcji to temat, który bardzo często pojawia się na maturze i który jednocześnie sprawia sporo problemów. Spróbujmy zatem omówić wszystkie kluczowe aspekty związanie z przekształceniami, tak aby rozwiać wszelkie wątpliwości.

Co to znaczy, że funkcja jest przekształcona?
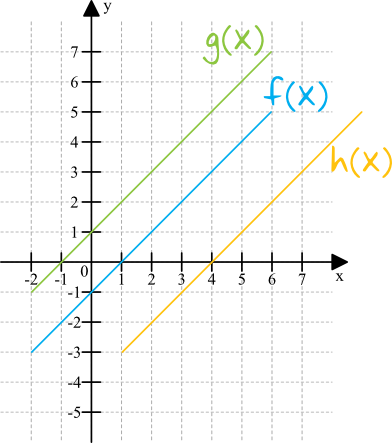
Zanim zaczniemy cokolwiek liczyć i analizować, to dobrze byłoby w ogóle ustalić czym tak naprawdę będziemy się zajmować w tym temacie. Wyobraźmy sobie, że mamy np. parabolę, która jest wykresem jakieś funkcji kwadratowej, która to parabola jest przesuwana o ileś jednostek w dowolną stronę. Przykładowo, na poniższym rysunku mamy wykres funkcji $f(x)$ oraz dwa dość podobne wykresy funkcji $g(x)$ oraz $h(x)$, które powstały w wyniku przesunięcia funkcji $f(x)$ w górę oraz w lewo:

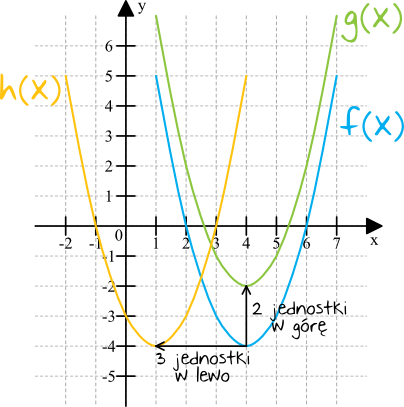
Widzimy, że zielona funkcja $g(x)$ jest przesunięta o $2$ jednostki w górę względem niebieskiej $f(x)$, natomiast pomarańczowa $h(x)$ jest przesunięta o $3$ jednostki w lewo względem niebieskiej $f(x)$. Sytuacja zaprezentowana na powyższym rysunku jest właśnie klasycznym przykładem przesunięć/przekształceń wykresu funkcji. W tym temacie będziemy analizować m.in. jak takie przekształcenia mogą wyglądać i jaki ma to wpływ na wzory oraz wykresy takich funkcji.

Tu przy okazji mała podpowiedź – analizując przesunięcia/przekształcenia, dobrze jest zwracać uwagę na najbardziej charakterystyczne punkty wykresu danej funkcji. W powyższym przykładzie takim idealnym odniesieniem był wierzchołek paraboli, ale mogą to być też miejsca przecięcia się z osią czy też różne załamania wykresu.

Jak można przekształcić wykres funkcji?
Istnieją zasadniczo trzy główne kategorie przekształceń, które interesują nas na lekcjach matematyki (na poziomie podstawowym):
· przesunięcia w górę/w dół;
· przesunięcia w lewo/w prawo;
· przekształcenia względem osi $OX$, osi $OY$ oraz początku układu współrzędnych.

Przesunięcia w górę/w dół
To zdecydowanie najłatwiejszy do omówienia rodzaj przekształcenia. Spójrzmy na poniższy rysunek, na którym znajduje się funkcja $f(x)$, która jest naszym punktem wyjścia oraz dwie nowe funkcje $g(x)$ oraz $h(x)$, które powstały w wyniku dokonania pewnych przesunięć.

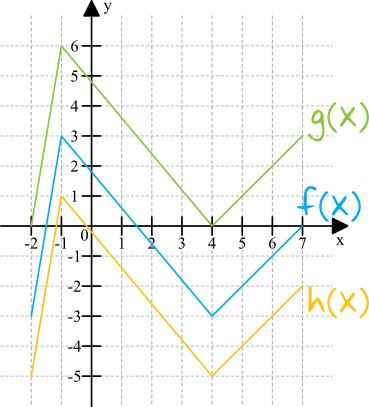
W pierwszym przypadku funkcja $f(x)$ została przesunięta o $3$ jednostki w górę, tworząc nową funkcję $g(x)$, a w drugim przypadku funkcja $f(x)$ została przesunięta o $2$ jednostki w dół, tworząc nową funkcję $h(x)$.

Teraz moglibyśmy zauważyć, że funkcja $g(x)$ dla każdego argumentu $x$ przyjmuje wartości o $3$ większe od funkcji $f(x)$. Tak przykładowo, funkcja $f(x)$ dla argumentu $x=7$ przyjmuje wartość $y=0$, natomiast dla tego samego argumentu funkcja $g(x)$ przyjmuje wartość $y=3$. Skoro więc funkcja $g(x)$ przyjmuje zawsze wartości o $3$ większe od funkcji $f(x)$, to matematycznie moglibyśmy zapisać, że:
$$g(x)=f(x)+3$$

Analogicznie funkcja $h(x)$ przyjmuje zawsze wartości o $2$ mniejsze od funkcji $f(x)$. Możemy porównać dowolne argumenty i zawsze przyjmowane dla nich wartości będą o $2$ mniejsze. Zapisalibyśmy zatem, że:
$$h(x)=f(x)-2$$

Przesunięcia w lewo/w prawo
Spójrzmy teraz na nowy rysunek, na którym znajduje się funkcja $f(x)$, względem której powstały dwie nowe funkcje $i(x)$ oraz $j(x)$.

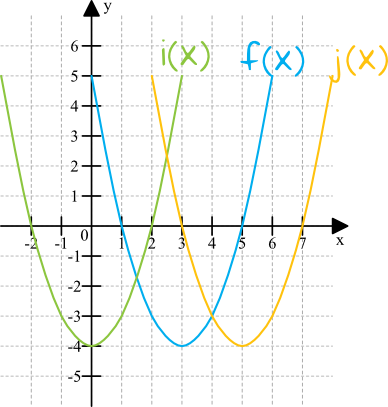
Tym razem funkcja $f(x)$ została przesunięta w lewo o $3$ jednostki, tworząc nową funkcję $i(x)$, a gdy przesunęliśmy ją w prawo o $2$ jednostki to powstała nam funkcja $j(x)$. Widać to bardzo dobrze po miejscach przecięcia się z osią $OX$ lub też po wierzchołku paraboli.

Tutaj możemy poczynić nieco inną obserwację niż przy przesunięciach w górę/w dół. Spójrzmy na funkcję $i(x)$. Wartość funkcji $i(x)$ dla danego argumentu $x$ jest taka sama, jak wartość funkcji $f(x)$ dla argumentu o $3$ większego. Przykładowo, funkcja $i(x)$ przyjmuje wartość równą $y=-4$ dla argumentu $x=0$, natomiast funkcja $f(x)$ tą samą wartość przyjmuje dla argumentu, który jest o $3$ większy, czyli dla $x=3$ To pozwala nam zapisać, że:
$$i(x)=f(x+3)$$

I analogicznie będzie w przypadku funkcji $j(x)$. Wartości przyjmowane dla poszczególnych argumentów są takie same, jak wartości funkcji $f(x)$ przyjmowane dla argumentów o $2$ mniejszych. W związku z tym:
$$j(x)=f(x-2)$$

Właśnie z przesunięciami w lewo/w prawo wiąże się najwięcej trudności, bo na pierwszy rzut oka wydają się one mniej intuicyjne jeśli chodzi o zapisywanie wzoru. Pamiętaj, że mając przesunięcie w lewo musimy w nawiasie dać znak dodawania, a mając przesunięcie w prawo dajemy w nawiasie znak odejmowania, mimo iż intuicja podpowiadałaby odwrotny mechanizm.

Przesunięcia w górę/w dół oraz w lewo/w prawo (jednocześnie)
Jak już opanujemy podstawowe przypadki, to możemy spotkać się z sytuacją, w której jakaś funkcja jest przesunięta zarówno w pionie oraz poziomie jednocześnie. Spójrzmy na poniższy przykład:

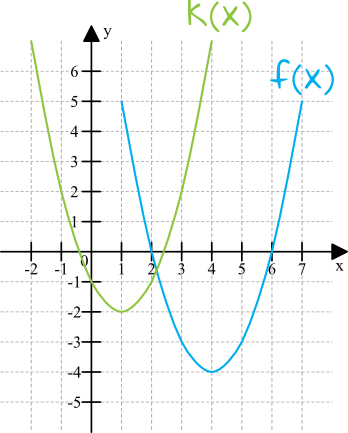
Widzimy tutaj funkcję $k(x)$, która powstała w wyniku przesunięcia funkcji $f(x)$ o $2$ jednostki w górę i $3$ jednostki w lewo. Dobrze to widać jeśli podążamy drogą jakiegoś charakterystycznego punktu – w tym przypadku idealnie sprawdza się wierzchołek paraboli. Wzór powyższej funkcji łączy w sobie to, co omawialiśmy w poprzednich podpunktach, zatem moglibyśmy zapisać, że:
$$k(x)=f(x+3)+2$$

Przekształcenia względem osi $OX$, $OY$ oraz początku układu współrzędnych
Tak jak do tej pory zajmowaliśmy się bardziej przesuwaniem wykresów, tak teraz będziemy je faktycznie przekształcać, sprawiając że czasem sam wykres będzie się sporo różnił od tego początkowego. Wyróżniamy trzy główne przekształcenia – względem osi $OX$, $OY$ oraz początku układu współrzędnych. Spójrzmy na poniższy przykład funkcji $f(x)$, która została przekształcona na każdy z tych trzech sposobów, tworząc nowe funkcje $l(x)$, $m(x)$ oraz $n(x)$:

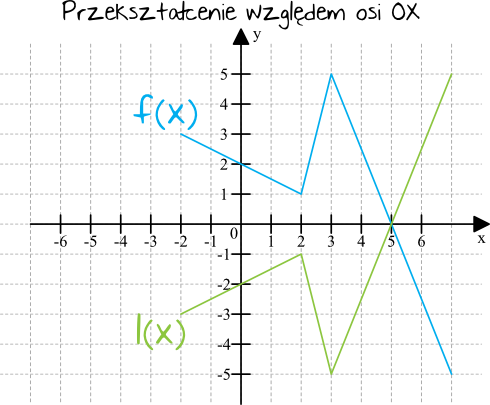
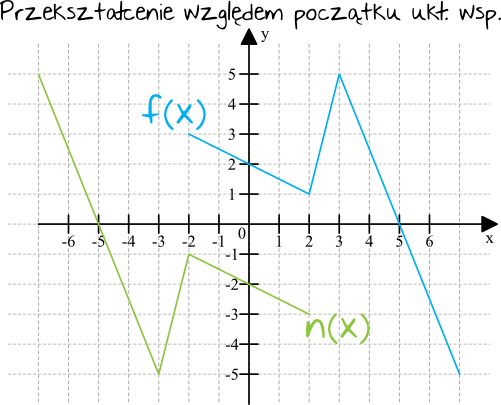
Przeanalizujmy teraz każdą z tych nowych funkcji. Zaczynamy od $l(x)$, która powstała w wyniku przekształcenia funkcji $f(x)$ względem osi $OX$. Widzimy, że przy przekształceniu względem osi $OX$ wszystkie wartości przyjmowane dla odpowiednich argumentów, zmieniły swój znak na przeciwny. Przykładowo funkcja $f(x)$ dla argumentu $x=3$ przyjmuje wartość $y=-5$, natomiast funkcja $l(x)$ przyjmuje wartość przeciwną, czyli $y=-5$. Zapisalibyśmy więc, że:
$$l(x)=-f(x)$$

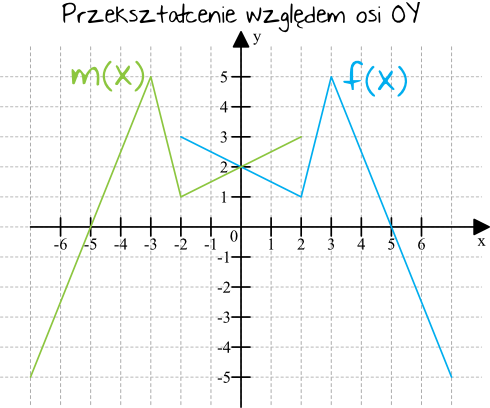
Teraz spójrzmy na funkcję $m(x)$, która powstała w wyniku przekształcenia funkcji $f(x)$ względem osi $OY$. W przypadku przekształcenia względem osi $OY$ mamy sytuację nieco odwrotną, czyli te same wartości są przyjmowane dla przeciwnych argumentów. Tak jak funkcja $f(x)$ przyjmowała wartość $y=5$ dla $x=3$, tak funkcja $m(x)$ przyjmuje tę wartość dla $x=-3$. Tu moglibyśmy zapisać, że:
$$m(x)=f(-x)$$

I na koniec funkcja $m(x)$, którą otrzymaliśmy przekształcając funkcję $f(x)$ względem początku układu współrzędnych. Przekształcenie względem początku układu współrzędnych łączy przekształcenia względem osi $OX$ oraz $OY$. Funkcja $f(x)$ dla argumentu $x=3$ przyjmowała wartość $y=5$, natomiast teraz dla argumentu $x=-3$ przyjmuje ona wartość $y=-5$. Tym samym:
$$n(x)=-f(-x)$$

Odczytywanie informacji ze wzorów przekształconych funkcji
Potrafimy już zapisywać relacje między przekształconymi funkcjami, to teraz w ramach treningu przeanalizujemy czynność odwrotną – czyli na podstawie wzoru, spróbujemy ustalić z jakim przesunięciem/przekształceniem mamy tutaj do czynienia.

Przykład 1. Ustal w jaki sposób należy przesunąć podaną funkcję $f(x)$, aby otrzymać funkcję $g(x)$, w każdym z poniższych przypadków:
a) $f(x)=x^2$ oraz $g(x)=(x-3)^2$
b) $f(x)=2^x$ oraz $g(x)=2^{x-3}$
c) $f(x)=\frac{2}{x}$ oraz $g(x)=\frac{2}{x}-3$
d) $f(x)=\sqrt{x}$ oraz $g(x)=\sqrt{x+3}+3$

Rozwiązanie:
a) Tutaj sprawa jest bardzo prosta, widzimy że w zapisie wzoru argument $x$ jest pomniejszony o $3$, czyli jest to klasyczny przypadek w którym funkcja $g(x)$ powstała w wyniku przesunięcia funkcji $f(x)$ o $3$ jednostki w prawo.
b) Wydaje się, że ten przykład jest bardziej skomplikowany, zwłaszcza że cała zmiana dzieje się w wykładniku potęgi, ale tak naprawdę mamy dokładnie tą samą historię co przed chwilą. Argument $x$ jest pomniejszony o $3$, czyli tutaj też funkcja $g(x)$ powstała w wyniku przesunięcia funkcji $f(x)$ o $3$ jednostki w prawo.
c) Tym razem widzimy, że na końcu zapisu pojawiło nam się $-3$, czyli wszystkie wartości funkcji $g(x)$ są o $3$ mniejsze od wartości funkcji $f(x)$. Możemy więc powiedzieć, że tutaj funkcja $g(x)$ powstała w wyniku przesunięcia funkcji $f(x)$ o $3$ jednostki w dół.
d) Najciekawszy przypadek, ponieważ mamy tutaj dwa przesunięcia jednocześnie. W zapisie funkcji $g(x)$ mamy argument $x$ powiększony o $3$, czyli będzie to przesunięcie o $3$ jednostki w lewo, a dodatkowo na końcu zapisu pojawia się $+3$, czyli cała funkcja jest jeszcze przesunięta o $3$ jednostki w górę.

Nasze wnioski na temat różnych funkcji nie muszą się ograniczać tylko do samego określania przesunięć. Jedną z ważniejszych obserwacji jest dostrzeżenie, że każde takie przekształcenie zmienia kluczowe parametry danej funkcji np. dziedzinę, zbiór wartości, miejsca zerowe, miejsca przecięcia się z osiami czy też położenie innych charakterystycznych punktów.

Przykład 2. Zbiorem wartości funkcji $f(x)$ jest przedział $\langle-3;5\rangle$. Ustal, jaki jest zbiór wartości funkcji $g(x)=f(x)+2$ oraz $h(x)=f(x-3)$.

Rozwiązanie:
Zacznijmy od funkcji $g(x)$, która jak widzimy jest przesunięta względem funkcji $f(x)$ o $2$ jednostki w górę. Skoro tak, to wszystkie wartości przyjmowane przez funkcję $g(x)$ będą o $2$ większe od funkcji $f(x)$, co z kolei sprawi, że zmieni się także zbiór wartości. Najmniejszą wartością nie będzie już $-3$, tylko będzie liczba o $2$ większa, czyli $-1$. I analogicznie największą wartością nie będzie już $5$, tylko $7$. To oznacza, że zbiorem wartości będzie przedział $\langle-1;7\rangle$.

To teraz funkcja $h(x)$, która jak widzimy po wzorze, jest przesunięta o $3$ jednostki w prawo. Jak takie przesunięcie wpłynie na zbiór wartości? Okazuje się, że takie przesunięcie w ogóle nie wpłynie na zbiór wartości. Funkcja $h(x)$ będzie przyjmować dokładnie takie same wartości jak funkcja $f(x)$, tylko będzie się to działo dla innych argumentów. W takim razie zbiorem wartości funkcji $h(x)$ będzie przedział $\langle-3;5\rangle$.

Jeżeli nie dostrzegasz za bardzo tych zależności, to poniżej możesz zobaczyć takie proste zobrazowanie tej całej sytuacji. Oczywiście nie wiemy jak dokładnie wygląda funkcja $f(x)$, więc ten rysunek jest bardzo umowny, ale pozwoli on zrozumieć dlaczego zmienił się zbiór wartości funkcji $g(x)$, a nie zmienił funkcji $h(x)$.
przekształcanie wykresów funkcji

Przykład 3. Funkcja $f(x)$ ma tylko jedno miejsce zerowe i jest nim $x=4$. Jakie miejsce zerowe ma funkcja $g(x)=f(x+3)$?.

Rozwiązanie:
Na początek przypomnienie – miejsce zerowe to argument, dla którego funkcja przyjmuje wartość równą $0$. Mówiąc bardzo obrazowo, jest to argument dla którego wykres funkcji przecina oś $OX$.

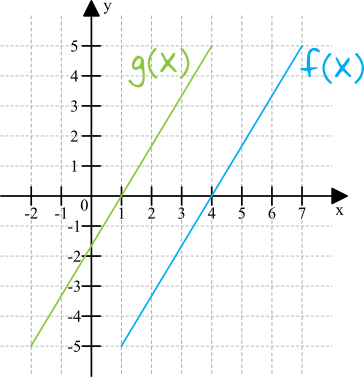
Ze wzoru wynika, że funkcja $g(x)$ jest przesunięciem funkcji $f(x)$ o $3$ jednostki w lewo. To oznacza, że cały wykres funkcji (czyli także nasze miejsce zerowe) przesunie się o $3$ jednostki w lewo. To sprawi, że miejscem zerowym funkcji $g(x)$ będzie liczba o $3$ mniejsza od $4$, czyli będzie to $x=1$.

I tu podobnie jak w poprzednim zadaniu, jeśli nie czujemy tej sytuacji, to możemy zrobić sobie taki „oszukany” rysunek przykładowej funkcji $f(x)$, która ma miejsce zerowe $x=4$. Jeżeli teraz przesuniemy tę funkcję o $3$ jednostki w lewo, to zobaczymy, że faktycznie miejscem zerowym będzie tym razem $x=1$.
przekształcanie wykresów funkcji

Zapisywanie pełnych wzorów przekształconych funkcji
Do tej pory wzory przesuniętych funkcji odnosiliśmy do funkcji $f(x)$, otrzymując zapisy typu $g(x)=f(x)+3$ czy też $g(x)=f(x-3)$. Takie zapisy są bardzo wygodne w temacie przekształceń, bo od razu widzimy z jakim przesunięciem mamy do czynienia. Pójdźmy jednak o krok dalej i spróbujmy zapisać wzory przekształconych funkcji w nieco bardziej tradycyjnej formie.

Wyobraźmy sobie, że mamy funkcję $f(x)=x^2-3x-4$ i spróbujmy teraz zapisać pełny wzór funkcji $a(x)$, która jest przesunięta o np. $5$ jednostek w górę. Wiemy już, że funkcja przesunięta o $5$ jednostek w górę to $a(x)=f(x)+5$, a podstawiając konkretny wzór funkcji $f(x)$ do tego zapisu, wyjdzie nam, że:
$$a(x)=x^2-3x-4+5 \\
a(x)=x^2-3x+1$$

To było dość łatwe, a jak będzie wyglądał wzór funkcji $b(x)$, która powstałaby np. w wyniku przesunięcia funkcji $f(x)=x^2-3x-4$ o $2$ jednostki w lewo? Jest to przesunięcie w lewo, czyli $b(x)=f(x+2)$. Mówiąc bardzo obrazowo, chcąc poznać wzór funkcji $b(x)$ musimy w miejsce $x$ podstawić wszędzie $x+2$. Zapisalibyśmy więc, że:
$$b(x)=(x+2)^2-3\cdot(x+2)-4 \\
b(x)=x^2+4x+4-3x-6-4 \\
b(x)=x^2+x-6$$

Tak omówić moglibyśmy każdy różnorodny przypadek, ale może żeby nie tworzyć tutaj niepotrzebnie dodatkowych opisów, przeanalizujmy zbiorczo różnorodne przypadki:

Przykład 4. Dana jest funkcja $f(x)=x^2-3$. Wyznacz wzór funkcji $g(x)$, która powstała w wyniku przesunięcia/przekształcenia:
a) o $5$ jednostek w górę
b) o $5$ jednostek w dół
c) o $5$ jednostek w lewo
d) o $5$ jednostek w prawo
e) o $5$ jednostek w dół i $5$ jednostek w prawo
f) względem osi $OX$
g) względem osi $OY$
h) względem początku układu współrzędnych

Rozwiązanie:
a) o $5$ jednostek w górę
$g(x)=f(x)+5 \\
g(x)=x^2-3+5 \\
g(x)=x^2+2$

b) o $5$ jednostek w dół
$g(x)=f(x)-5 \\
g(x)=x^2-3-5 \\
g(x)=x^2-8$

c) o $5$ jednostek w lewo
$g(x)=f(x+5) \\
g(x)=(x+5)^2-3 \\
g(x)=x^2+10x+25-3 \\
g(x)=x^2+10x+22$

d) o $5$ jednostek w prawo
$g(x)=f(x-5) \\
g(x)=(x-5)^2-3 \\
g(x)=x^2-10x+25-3 \\
g(x)=x^2-10x+22$

e) o $5$ jednostek w dół i $5$ jednostek w prawo
$g(x)=f(x-5)-5 \\
g(x)=(x-5)^2-3-5 \\
g(x)=x^2-10x+25-3-5 \\
g(x)=x^2-10x+17$

f) względem osi $OX$
$g(x)=-f(x) \\
g(x)=-(x^2-3) \\
g(x)=-x^2+3$

g) względem osi $OY$
$g(x)=f(-x) \\
g(x)=(-x)^2-3 \\
g(x)=x^2-3$

h) względem początku układu współrzędnych
$g(x)=-f(-x) \\
g(x)=-\left((-x)^2-3\right) \\
g(x)=-(x^2-3) \\
g(x)=-x^2+3$

Zobacz także:

Przekształcenia wykresów funkcji – Sprawdzian – Liceum, technikum (10 zadań)

Przekształcenia funkcji – lekcja video (kurs maturalny)

Przekształcenia funkcji – zadania maturalne

Funkcja liniowa

Funkcja kwadratowa